Comprehensive Guide to Adjacency Lists in Data Structures

In computer science, representing graphs effectively is crucial for performing many important operations and algorithms. One of the most widely used representations is the Adjacency List, which offers an efficient way to model sparse graphs. This article delves into the concepts behind the adjacency list, its representation, and how it compares to other techniques. Additionally, it explores practical implementations in several programming languages, such as Python, C, C++, C#, Java, PHP, and JavaScript.

What is an Adjacency List?

An Adjacency List is a way of representing a graph as an array of lists. Each list corresponds to a vertex in the graph and stores the vertices adjacent to that particular vertex. For a graph with n vertices, an adjacency list contains n entries, where each entry is a linked list or a dynamic array containing the neighboring vertices.

In simpler terms:

Each vertex has its own list (or array) that holds its adjacent vertices.
For undirected graphs, each edge is represented twice, as both vertices are neighbors.
For directed graphs, the list at vertex u contains v only if there is an edge directed from u to v.

Video credit: Bro Code

Understanding Adjacency Lists through Example

Undirected Graph Representation

Graph Representation of Undirected Graph to Adjacency List

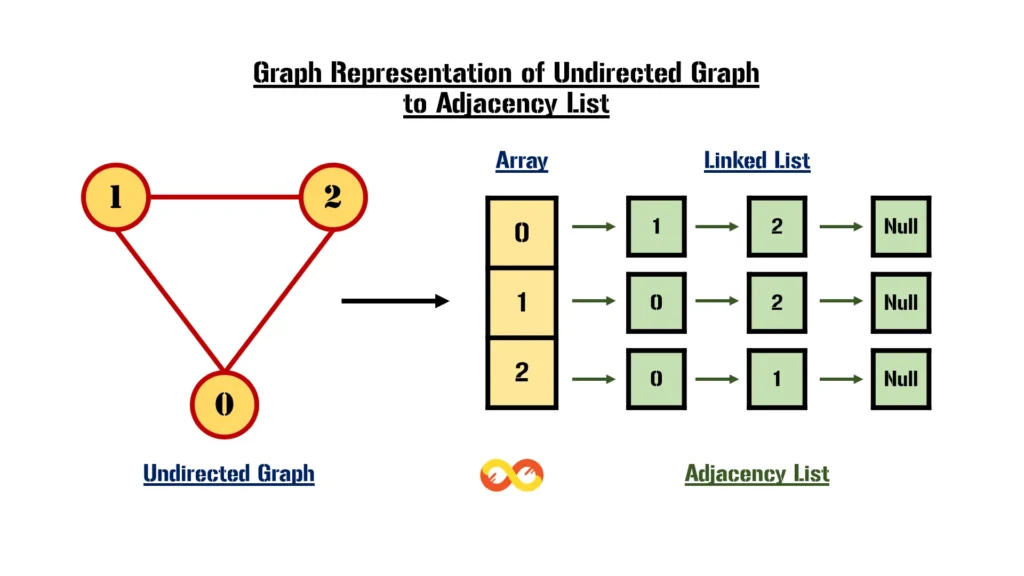
Let’s consider an undirected graph with three vertices (0, 1, and 2) and the following edges:

Vertex 0 is connected to vertices 1 and 2.
Vertex 1 is connected to vertices 0 and 2.
Vertex 2 is connected to vertices 0 and 1.

This can be represented as follows in an Adjacency List:

adjList[0] → [1, 2]
adjList[1] → [0, 2]
adjList[2] → [0, 1]

This structure clearly shows the adjacency relationships between vertices.

Directed Graph Representation

For a directed graph, let’s modify the previous example to have directed edges:

Vertex 0 has no outgoing edges.
Vertex 1 has edges directed to vertices 0 and 2.
Vertex 2 has an edge directed to vertex 0.

The adjacency list representation would be:

adjList[0] → []
adjList[1] → [0, 2]
adjList[2] → [0]

This list demonstrates the directed nature of the edges, with vertex 0 having no outgoing edges, while vertex 1 points to vertices 0 and 2.

Characteristics of Adjacency Lists

Size: The size of the adjacency list depends on the number of vertices (n) and the number of edges (m) in the graph. For each vertex, there is a list of its adjacent vertices.
Sparse Graphs: The adjacency list is particularly efficient for sparse graphs where the number of edges is much less than the square of the number of vertices (i.e., m << n²).
Time Complexity: Accessing a particular vertex’s neighbors in an adjacency list takes O(k), where k is the degree of the vertex.
Memory Usage: Adjacency lists use less memory compared to adjacency matrices, especially in sparse graphs, as only the edges are stored.

How to Build an Adjacency List?

Building an adjacency list for a graph involves the following steps:

Create an array of lists: Each index in the array represents a vertex, and each element in the array is a list of adjacent vertices.
Populate the adjacency lists: For each edge (u, v) in the graph:
- Add v to the list at index u.
- If the graph is undirected, also add u to the list at index v.
- If the graph is directed, only add v to the list at index u.

In the case of weighted graphs, store the weight of each edge alongside the connection in the adjacency list.

Applications of Adjacency Lists

Graph Algorithms: Many key algorithms, such as Dijkstra’s Shortest Path, Breadth-First Search (BFS), and Depth-First Search (DFS), rely on the adjacency list to efficiently traverse or search graphs.
Image Processing: Adjacency lists can be used to represent the connections between pixels in an image, where each pixel has neighbors that it connects to (e.g., the pixels adjacent to it in a grid).
Game Development: Graphs are often used in game maps, where each node represents a different area, and edges represent the connections between areas. Adjacency lists help efficiently store and traverse these connections.

Advantages of Using Adjacency Lists

Memory Efficiency: For sparse graphs, adjacency lists are much more space-efficient than adjacency matrices, as only existing edges are stored.
Easy Edge Addition and Removal: Modifying the graph structure, such as adding or removing edges, is fast and straightforward with adjacency lists.
Efficient Traversal: For graph traversal algorithms like BFS and DFS, adjacency lists provide efficient access to neighbors.

Disadvantages of Adjacency Lists

Slow Edge Lookup: While adjacency lists are efficient for most operations, checking for the existence of an edge between two arbitrary vertices takes O(k) time, where k is the number of neighbors of the vertex.
Memory Usage in Dense Graphs: For dense graphs, where the number of edges is close to n², an adjacency list might require more memory than an adjacency matrix.

Programming Examples of Adjacency List Implementation

Python Implementation

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.adj_list = [[] for _ in range(vertices)]

    def add_edge(self, u, v):
        self.adj_list[u].append(v)
        self.adj_list[v].append(u)  # Omit this line for directed graphs

    def display(self):
        for i in range(self.V):
            print(f"Vertex {i}: {self.adj_list[i]}")

# Example Usage
graph = Graph(3)
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
graph.display()

Output:

Vertex 0: [1, 2]
Vertex 1: [0, 2]
Vertex 2: [0, 1]

C Implementation

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int vertex;
    struct Node* next;
};

struct Graph {
    int numVertices;
    struct Node** adjLists;
};

struct Node* createNode(int v) {
    struct Node* newNode = malloc(sizeof(struct Node));
    newNode->vertex = v;
    newNode->next = NULL;
    return newNode;
}

struct Graph* createGraph(int vertices) {
    struct Graph* graph = malloc(sizeof(struct Graph));
    graph->numVertices = vertices;
    graph->adjLists = malloc(vertices * sizeof(struct Node*));

    for (int i = 0; i < vertices; i++) {
        graph->adjLists[i] = NULL;
    }

    return graph;
}

void addEdge(struct Graph* graph, int u, int v) {
    struct Node* newNode = createNode(v);
    newNode->next = graph->adjLists[u];
    graph->adjLists[u] = newNode;

    newNode = createNode(u);
    newNode->next = graph->adjLists[v];
    graph->adjLists[v] = newNode;
}

void printGraph(struct Graph* graph) {
    for (int v = 0; v < graph->numVertices; v++) {
        struct Node* temp = graph->adjLists[v];
        printf("Vertex %d:\n", v);
        while (temp) {
            printf(" %d ->", temp->vertex);
            temp = temp->next;
        }
        printf(" NULL\n");
    }
}

int main() {
    struct Graph* graph = createGraph(3);
    addEdge(graph, 0, 1);
    addEdge(graph, 0, 2);
    addEdge(graph, 1, 2);

    printGraph(graph);
    return 0;
}

Output:

Vertex 0:
 2 -> 1 -> NULL
Vertex 1:
 2 -> 0 -> NULL
Vertex 2:
 1 -> 0 -> NULL

C++ Implementation

#include <iostream>
#include <vector>
using namespace std;

class Graph {
    int V;
    vector<int>* adj;

public:
    Graph(int V) {
        this->V = V;
        adj = new vector<int>[V];
    }

    void addEdge(int u, int v) {
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    void display() {
        for (int i = 0; i < V; i++) {
            cout << "Vertex " << i << ":";
            for (int j : adj[i]) {
                cout << " " << j;
            }
            cout << endl;
        }
    }
};

int

 main() {
    Graph graph(3);
    graph.addEdge(0, 1);
    graph.addEdge(0, 2);
    graph.addEdge(1, 2);
    graph.display();

    return 0;
}

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

Java Implementation

import java.util.LinkedList;

public class Graph {
    private int V;
    private LinkedList<Integer> adjList[];

    public Graph(int vertices) {
        V = vertices;
        adjList = new LinkedList[vertices];
        for (int i = 0; i < vertices; i++) {
            adjList[i] = new LinkedList<>();
        }
    }

    public void addEdge(int u, int v) {
        adjList[u].add(v);
        adjList[v].add(u);  // Omit for directed graphs
    }

    public void display() {
        for (int i = 0; i < V; i++) {
            System.out.print("Vertex " + i + ": ");
            for (Integer vertex : adjList[i]) {
                System.out.print(vertex + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        Graph graph = new Graph(3);
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);
        graph.display();
    }
}

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

C# Implementation

using System;
using System.Collections.Generic;

class Graph {
    int V;
    List<int>[] adjList;

    public Graph(int vertices) {
        V = vertices;
        adjList = new List<int>[V];
        for (int i = 0; i < V; i++) {
            adjList[i] = new List<int>();
        }
    }

    public void AddEdge(int u, int v) {
        adjList[u].Add(v);
        adjList[v].Add(u);
    }

    public void Display() {
        for (int i = 0; i < V; i++) {
            Console.Write("Vertex " + i + ": ");
            foreach (var vertex in adjList[i]) {
                Console.Write(vertex + " ");
            }
            Console.WriteLine();
        }
    }

    static void Main(string[] args) {
        Graph graph = new Graph(3);
        graph.AddEdge(0, 1);
        graph.AddEdge(0, 2);
        graph.AddEdge(1, 2);
        graph.Display();
    }
}

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

PHP Implementation

<?php
class Graph {
    private $adjList;

    public function __construct($vertices) {
        $this->adjList = array_fill(0, $vertices, []);
    }

    public function addEdge($u, $v) {
        $this->adjList[$u][] = $v;
        $this->adjList[$v][] = $u;
    }

    public function display() {
        foreach ($this->adjList as $vertex => $neighbors) {
            echo "Vertex $vertex: " . implode(" ", $neighbors) . "\n";
        }
    }
}

$graph = new Graph(3);
$graph->addEdge(0, 1);
$graph->addEdge(0, 2);
$graph->addEdge(1, 2);
$graph->display();
?>

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

JavaScript Implementation

class Graph {
    constructor(vertices) {
        this.V = vertices;
        this.adjList = new Array(vertices).fill(0).map(() => []);
    }

    addEdge(u, v) {
        this.adjList[u].push(v);
        this.adjList[v].push(u);
    }

    display() {
        for (let i = 0; i < this.V; i++) {
            console.log(`Vertex ${i}: ${this.adjList[i].join(' ')}`);
        }
    }
}

let graph = new Graph(3);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.display();

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

Conclusion

The Adjacency List is a flexible and efficient way to represent sparse graphs, making it suitable for numerous applications in computer science. By storing only the edges that exist, it saves memory and is easy to traverse, particularly in algorithms like BFS, DFS, and Dijkstra’s. While there are certain disadvantages when it comes to edge lookups and dense graphs, the benefits in most practical cases, especially for sparse graphs, far outweigh these concerns.

As demonstrated, adjacency lists are not only conceptually simple but also easy to implement in multiple programming languages like Python, C, C++, Java, C#, PHP, and JavaScript. These implementations highlight the versatility and importance of adjacency lists in graph representation, reinforcing their position as a go-to method in data structures.

Frequently Asked Questions (FAQs) on Adjacency Lists in Data Structures

What is an Adjacency List in Data Structures?

An Adjacency List is a graph representation technique used to store information about a graph’s edges in the form of lists. For each vertex in the graph, there is a list that contains all of its adjacent (or neighboring) vertices. Each vertex is associated with a linked list or dynamic array to store the vertices it’s connected to.

Example:

Consider an undirected graph with three vertices (0, 1, and 2), and the following edges:

Vertex 0 is connected to vertex 1 and vertex 2.
Vertex 1 is connected to vertex 0 and vertex 2.
Vertex 2 is connected to vertex 0 and vertex 1.

This is how the Adjacency List would look:

adjList[0] → [1, 2]
adjList[1] → [0, 2]
adjList[2] → [0, 1]

In this format, the adjacency list stores the vertices that each node is connected to, enabling efficient traversal and search operations.

What is the difference between an Adjacency List and an Adjacency Matrix?

An Adjacency List stores only the existing edges in the graph, while an Adjacency Matrix is a 2D matrix where each cell represents the presence or absence of an edge between two vertices.

Key Differences:

Space Complexity:
- Adjacency List: Efficient in terms of space for sparse graphs where the number of edges (m) is much smaller than the number of vertices squared (n²). Space complexity is O(n + m).
- Adjacency Matrix: Space complexity is O(n²), regardless of how many edges are present.
Time Complexity:
- In an Adjacency List, accessing all adjacent vertices of a given vertex is O(k), where k is the degree of the vertex. Checking the existence of an edge takes O(k).
- In an Adjacency Matrix, accessing whether two vertices are connected is O(1).

How can you represent a Directed Graph using an Adjacency List?

In a Directed Graph, edges have direction. This means that if there is an edge from vertex u to vertex v, the adjacency list for u contains v, but the adjacency list for v will not necessarily contain u unless the reverse edge exists.

Example:

For a graph with three vertices:

Vertex 0 has an edge directed to vertex 2.
Vertex 1 has edges directed to vertex 0 and vertex 2.
Vertex 2 has no outgoing edges.

The adjacency list will be:

adjList[0] → [2]
adjList[1] → [0, 2]
adjList[2] → []

In this representation, each vertex’s list only contains the vertices it points to.

How do you implement an Adjacency List in Python?

In Python, an adjacency list can be implemented using lists of lists or dictionaries of lists.

Example Python Code:

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.adj_list = [[] for _ in range(vertices)]

    def add_edge(self, u, v):
        self.adj_list[u].append(v)
        self.adj_list[v].append(u)  # Omit this for directed graphs

    def display(self):
        for i in range(self.V):
            print(f"Vertex {i}: {self.adj_list[i]}")

graph = Graph(3)
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
graph.display()

Output:

Vertex 0: [1, 2]
Vertex 1: [0, 2]
Vertex 2: [0, 1]

This Python implementation uses a list of lists, where each inner list represents the adjacent vertices of a specific vertex.

How do you implement an Adjacency List in C?

In C, you can use a combination of arrays and linked lists to implement an adjacency list.

Example C Code:

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int vertex;
    struct Node* next;
};

struct Graph {
    int numVertices;
    struct Node** adjLists;
};

struct Node* createNode(int v) {
    struct Node* newNode = malloc(sizeof(struct Node));
    newNode->vertex = v;
    newNode->next = NULL;
    return newNode;
}

struct Graph* createGraph(int vertices) {
    struct Graph* graph = malloc(sizeof(struct Graph));
    graph->numVertices = vertices;
    graph->adjLists = malloc(vertices * sizeof(struct Node*));

    for (int i = 0; i < vertices; i++) {
        graph->adjLists[i] = NULL;
    }

    return graph;
}

void addEdge(struct Graph* graph, int u, int v) {
    struct Node* newNode = createNode(v);
    newNode->next = graph->adjLists[u];
    graph->adjLists[u] = newNode;

    newNode = createNode(u);
    newNode->next = graph->adjLists[v];
    graph->adjLists[v] = newNode;
}

void printGraph(struct Graph* graph) {
    for (int v = 0; v < graph->numVertices; v++) {
        struct Node* temp = graph->adjLists[v];
        printf("Vertex %d: ", v);
        while (temp) {
            printf("%d -> ", temp->vertex);
            temp = temp->next;
        }
        printf("NULL\n");
    }
}

int main() {
    struct Graph* graph = createGraph(3);
    addEdge(graph, 0, 1);
    addEdge(graph, 0, 2);
    addEdge(graph, 1, 2);

    printGraph(graph);
    return 0;
}

Output:

Vertex 0: 2 -> 1 -> NULL
Vertex 1: 2 -> 0 -> NULL
Vertex 2: 1 -> 0 -> NULL

Here, we use a linked list for each vertex’s neighbors, making it easier to store varying numbers of edges per vertex.

How do you implement an Adjacency List in C++?

In C++, an adjacency list can be implemented using vectors.

Example C++ Code:

#include <iostream>
#include <vector>
using namespace std;

class Graph {
    int V;
    vector<int>* adj;

public:
    Graph(int V) {
        this->V = V;
        adj = new vector<int>[V];
    }

    void addEdge(int u, int v) {
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    void display() {
        for (int i = 0; i < V; i++) {
            cout << "Vertex " << i << ": ";
            for (int j : adj[i]) {
                cout << j << " ";
            }
            cout << endl;
        }
    }
};

int main() {
    Graph graph(3);
    graph.addEdge(0, 1);
    graph.addEdge(0, 2);
    graph.addEdge(1, 2);
    graph.display();

    return 0;
}

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

This implementation uses vectors to store the adjacency list, which is ideal for dynamic memory management and efficient edge addition.

How do you implement an Adjacency List in Java?

In Java, an adjacency list can be implemented using LinkedLists.

Example Java Code:

import java.util.LinkedList;

public class Graph {
    private int V;
    private LinkedList<Integer>[] adjList;

    // Constructor for Graph
    public Graph(int vertices) {
        V = vertices;
        adjList = new LinkedList[vertices];
        for (int i = 0; i < vertices; i++) {
            adjList[i] = new LinkedList<>();
        }
    }

    // Add an edge to the graph
    public void addEdge(int u, int v) {
        adjList[u].add(v);
        adjList[v].add(u);  // Comment this line if the graph is directed
    }

    // Display the adjacency list representation of the graph
    public void display() {
        for (int i = 0; i < V; i++) {
            System.out.print("Vertex " + i + ": ");
            for (Integer vertex : adjList[i]) {
                System.out.print(vertex + " ");
            }
            System.out.println();
        }
    }

    // Main method to test the graph
    public static void main(String[] args) {
        Graph graph = new Graph(3);
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);

        graph.display();
    }
}

Output is...
Vertex 0: 1 2 
Vertex 1: 0 2 
Vertex 2: 0 1

How do you implement an Adjacency List in C#?

In C#, an adjacency list can be implemented using the List class from the System.Collections.Generic namespace, which provides a dynamic array structure.

Example C# Code:

using System;
using System.Collections.Generic;

class Graph {
    int V;
    List<int>[] adjList;

    public Graph(int vertices) {
        V = vertices;
        adjList = new List<int>[V];
        for (int i = 0; i < V; i++) {
            adjList[i] = new List<int>();
        }
    }

    public void AddEdge(int u, int v) {
        adjList[u].Add(v);
        adjList[v].Add(u);  // Omit this line for directed graphs
    }

    public void Display() {
        for (int i = 0; i < V; i++) {
            Console.Write("Vertex " + i + ": ");
            foreach (var vertex in adjList[i]) {
                Console.Write(vertex + " ");
            }
            Console.WriteLine();
        }
    }

    static void Main(string[] args) {
        Graph graph = new Graph(3);
        graph.AddEdge(0, 1);
        graph.AddEdge(0, 2);
        graph.AddEdge(1, 2);
        graph.Display();
    }
}

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

The List class in C# offers dynamic sizing for managing adjacency lists, ensuring efficient edge insertion and traversal.

How do you implement an Adjacency List in PHP?

In PHP, adjacency lists can be implemented using arrays to store neighboring vertices.

Example PHP Code:

<?php
class Graph {
    private $adjList;

    public function __construct($vertices) {
        $this->adjList = array_fill(0, $vertices, []);
    }

    public function addEdge($u, $v) {
        $this->adjList[$u][] = $v;
        $this->adjList[$v][] = $u;  // Omit this line for directed graphs
    }

    public function display() {
        foreach ($this->adjList as $vertex => $neighbors) {
            echo "Vertex $vertex: " . implode(" ", $neighbors) . "\n";
        }
    }
}

$graph = new Graph(3);
$graph->addEdge(0, 1);
$graph->addEdge(0, 2);
$graph->addEdge(1, 2);
$graph->display();
?>

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

PHP arrays are used to represent adjacency lists, allowing for dynamic edge storage and straightforward indexing.

How do you implement an Adjacency List in JavaScript?

In JavaScript, adjacency lists can be implemented using arrays, which dynamically store the neighbors of each vertex.

Example JavaScript Code:

class Graph {
    constructor(vertices) {
        this.V = vertices;
        this.adjList = Array.from({ length: vertices }, () => []);
    }

    addEdge(u, v) {
        this.adjList[u].push(v);
        this.adjList[v].push(u);  // Omit this line for directed graphs
    }

    display() {
        this.adjList.forEach((neighbors, index) => {
            console.log(`Vertex ${index}: ${neighbors.join(' ')}`);
        });
    }
}

let graph = new Graph(3);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.display();

Output:

Vertex 0: 1 2
Vertex 1: 0 2
Vertex 2: 0 1

JavaScript’s arrays provide a simple and efficient way to manage adjacency lists, leveraging their dynamic nature.

What are the advantages of using an Adjacency List?

Adjacency Lists offer several benefits, particularly in the context of sparse graphs:

Space Efficiency: They require O(n + m) space, where n is the number of vertices and m is the number of edges. This is more space-efficient for sparse graphs compared to adjacency matrices.
Dynamic Edge Management: Inserting and removing edges is straightforward.
Efficient Neighbor Traversal: Accessing adjacent vertices takes O(k) time, where k is the number of neighbors.
Flexibility: Adjacency lists can easily be modified to represent weighted graphs.

What are the disadvantages of using an Adjacency List?

Despite their advantages, Adjacency Lists have some downsides:

Edge Lookup Time: Checking for the existence of a specific edge takes O(k) time, where k is the number of neighbors. In contrast, adjacency matrices offer constant time lookup O(1).
Inefficiency for Dense Graphs: Adjacency lists are less efficient in terms of space and time when the graph is dense (i.e., close to n² edges).
Complex Algorithm Implementation: Some algorithms are more complicated to implement with adjacency lists compared to adjacency matrices.

How do you modify an Adjacency List for Weighted Graphs?

In weighted graphs, each edge has an associated weight. To represent this in an adjacency list, store pairs of vertices and their corresponding weights.

Example Python Code for Weighted Graph:

class WeightedGraph:
    def __init__(self, vertices):
        self.V = vertices
        self.adj_list = [[] for _ in range(vertices)]

    def add_edge(self, u, v, weight):
        self.adj_list[u].append((v, weight))
        self.adj_list[v].append((u, weight))  # Omit this for directed graphs

    def display(self):
        for i in range(self.V):
            print(f"Vertex {i}: {self.adj_list[i]}")

graph = WeightedGraph(3)
graph.add_edge(0, 1, 4)
graph.add_edge(0, 2, 5)
graph.add_edge(1, 2, 6)
graph.display()

Output:

Vertex 0: [(1, 4), (2, 5)]
Vertex 1: [(0, 4), (2, 6)]
Vertex 2: [(0, 5), (1, 6)]

In this approach, each entry in the adjacency list is a tuple containing a vertex and the weight of the edge.

How do you traverse a graph using an Adjacency List?

Graph traversal can be done using either Breadth-First Search (BFS) or Depth-First Search (DFS).

BFS Example in Python:

from collections import deque

def bfs(graph, start):
    visited = [False] * len(graph.adj_list)
    queue = deque([start])
    visited[start] = True

    while queue:
        vertex = queue.popleft()
        print(vertex, end=" ")

        for neighbor in graph.adj_list[vertex]:
            if not visited[neighbor]:
                visited[neighbor] = True
                queue.append(neighbor)

graph = Graph(3)
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
bfs(graph, 0)

Output:

0 1 2

DFS Example in Python:

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start, end=" ")

    for neighbor in graph.adj_list[start]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

graph = Graph(3)
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
dfs(graph, 0)

Output:

0 1 2

How can you count the number of edges in a graph using an Adjacency List?

To count the number of edges in an undirected graph, iterate through the adjacency list and count each edge, remembering that each edge is counted twice.

Example Python Code:

def count_edges(graph):
    edge_count = 0
    for neighbors in graph.adj_list:
        edge_count += len(neighbors)
    return edge_count // 2

graph = Graph(3)
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
print("Number of edges:", count_edges(graph))

Output:

Number of edges: 3

For directed graphs, simply count all edges directly without dividing by 2.

Can an Adjacency List be used for a Weighted Directed Graph?

Yes, an adjacency list can represent a weighted directed graph. Instead of storing pairs of vertices and weights, each list entry would store only the outgoing edges and their weights.

Example Python Code for Weighted Directed Graph:

class WeightedDirectedGraph:
    def __init__(self, vertices):
        self.V = vertices
        self.adj_list = [[] for _ in range(vertices)]

    def add_edge(self, u, v, weight):
        self.adj_list[u].append((v, weight))

    def display(self):
        for i in range(self.V):
            print(f"Vertex {i}: {self.adj_list[i]}")

graph = WeightedDirectedGraph(3)
graph.add_edge(0, 1, 4)
graph.add_edge(0, 2, 5)
graph.add_edge(1, 2, 6)
graph.display()

Output:

Vertex 0: [(1, 4), (2, 5)]
Vertex 1: [(2, 6)]
Vertex 2: []

In this example, directed edges are stored without duplication, allowing for a more efficient representation.

Comprehensive Guide to Adjacency Lists in Data Structures

Table of Contents

What is an Adjacency List?

Understanding Adjacency Lists through Example

Undirected Graph Representation

Directed Graph Representation

Characteristics of Adjacency Lists

How to Build an Adjacency List?

Applications of Adjacency Lists

Advantages of Using Adjacency Lists

Disadvantages of Adjacency Lists

Programming Examples of Adjacency List Implementation

Python Implementation

C Implementation

C++ Implementation

Java Implementation

C# Implementation

PHP Implementation

JavaScript Implementation

Conclusion

Related Articles

Read More Articles

Frequently Asked Questions (FAQs) on Adjacency Lists in Data Structures

What is an Adjacency List in Data Structures?

Example:

What is the difference between an Adjacency List and an Adjacency Matrix?

Key Differences:

How can you represent a Directed Graph using an Adjacency List?

Example:

How do you implement an Adjacency List in Python?

Example Python Code:

How do you implement an Adjacency List in C?

Example C Code:

How do you implement an Adjacency List in C++?

Example C++ Code:

How do you implement an Adjacency List in Java?

Example Java Code:

How do you implement an Adjacency List in C#?

Example C# Code:

How do you implement an Adjacency List in PHP?

Example PHP Code:

How do you implement an Adjacency List in JavaScript?

Example JavaScript Code:

What are the advantages of using an Adjacency List?

What are the disadvantages of using an Adjacency List?

How do you modify an Adjacency List for Weighted Graphs?

Example Python Code for Weighted Graph:

How do you traverse a graph using an Adjacency List?

BFS Example in Python:

DFS Example in Python:

How can you count the number of edges in a graph using an Adjacency List?

Example Python Code:

Can an Adjacency List be used for a Weighted Directed Graph?

Example Python Code for Weighted Directed Graph: