Understanding Weighted Graphs: A Comprehensive Exploration

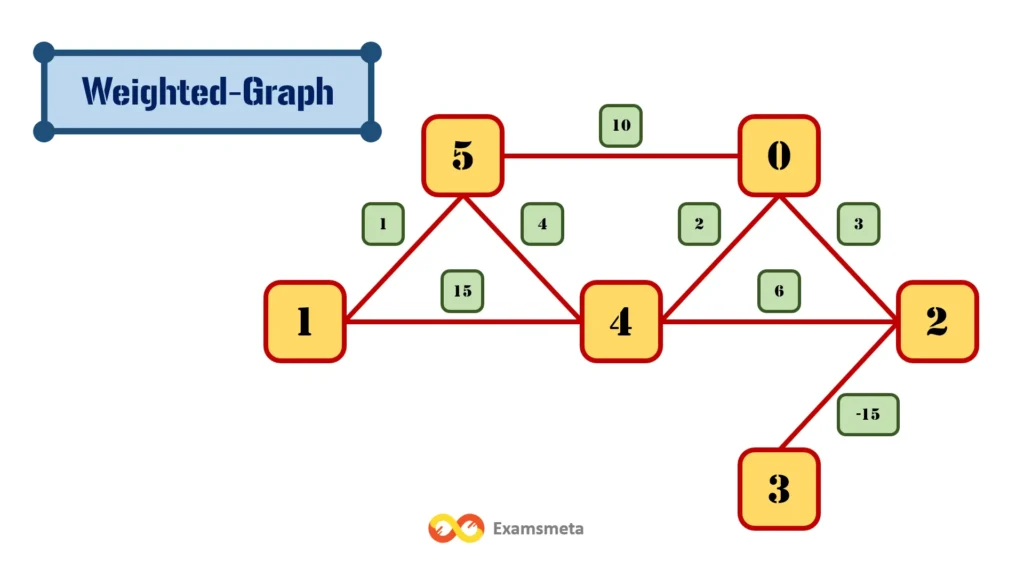
What is a Weighted Graph?

A weighted graph is a specialized type of graph where each edge is assigned a weight or value. These weights can represent a wide range of real-world entities, such as cost, distance, capacity, or any other relative measurement. The concept of a weighted graph is integral to various fields such as computer science, mathematics, and engineering, as it provides a structured way to model problems that involve relationships between objects.

Weighted graphs are often represented using adjacency matrices or adjacency lists. The weights, which are typically non-negative integers or real numbers, provide additional context about the relationship between nodes. For example, in a road network, the edges of a weighted graph could represent roads, while the weights represent the distance or travel time between locations (nodes).

Applications of Weighted Graphs

2D Matrix Games

In two-dimensional matrix-based games, a weighted graph can help find the optimal path between the starting and ending points. The graph’s weights represent factors such as time, cost, or effort, which can be used to solve problems like finding the maximum sum along a path. A popular example of such problems is the grid-based pathfinding algorithm where each step has an associated cost, and the goal is to minimize or maximize the total cost of the path.

Spanning Trees

A minimum spanning tree (MST) is a subgraph of a weighted graph that connects all vertices together with the minimum total edge weight and no cycles. Algorithms such as Kruskal’s and Prim’s are widely used to find the MST, which is essential in various network design applications such as laying out cable or pipeline networks to minimize total cost.

Constraint Graphs

Weighted graphs are widely used to represent constraints in systems like scheduling, product design, or artificial intelligence. These graphs are helpful when multiple items need to be coordinated, and each constraint is represented by a weighted edge. In scheduling problems, the graph can help optimize the overall cost or time by modeling dependencies between tasks.

Dependency Graphs

Directed weighted graphs are extensively used to represent dependencies between various components in complex systems. For example, in large-scale software projects, tasks have dependencies on each other, and the weights represent the precedence or priority. These graphs help project managers or AI systems minimize completion time while satisfying dependencies. Examples include software build dependency graphs and pipeline execution order.

Compilers

Compilers use weighted graphs for various optimizations such as data flow analysis, where a graph’s vertices represent program variables or statements, and edges represent the flow of information between them. The weights can be used for analyzing the cost of operations or for determining the optimal query execution plan in database systems. Type inference algorithms and register allocation also heavily rely on weighted graphs.

Artificial Intelligence

In AI, weighted graphs are often used in decision-making processes like game trees where each node represents a possible state of the game and the edges represent transitions between states. The weights on the edges signify the cost or reward associated with making a particular move. Popular AI algorithms such as Minimax and Alpha-Beta Pruning use weighted graphs to decide the best strategy for a player in a two-player game.

Image Processing

In image processing, weighted graphs can be used for segmentation. Here, the graph’s vertices represent the pixels of an image, and the edges between them have weights representing the similarity between pixels, based on characteristics such as color or brightness. Algorithms like graph cuts leverage weighted graphs for image segmentation, where they partition the image into different segments.

Natural Language Processing

In natural language processing (NLP), weighted graphs can represent relationships between words, where the edges’ weights signify the strength of the relationship (e.g., semantic similarity). Graph-based techniques like TextRank use weighted graphs to extract the most important words or sentences from a text, making them vital in tasks like text summarization and keyword extraction.

Real-World Applications of Weighted Graphs

Transportation Networks

In transportation networks, weighted graphs help optimize routes by minimizing travel time, distance, or cost. Google Maps, Bing Maps, and GPS systems rely on weighted graphs for pathfinding algorithms like Dijkstra’s or A* Search to provide users with the most efficient routes. These graphs also play a critical role in traffic analysis, allowing companies like Uber and Lyft to model traffic patterns and predict arrival times.

Document Link Graphs

In search engines, link-weighted graphs are used to analyze the relevance of web pages. The weight of the edges between pages can represent factors like the number of links, frequency of access, or PageRank, which helps identify the most authoritative sources of information.

Epidemiology

In epidemiology, weighted graphs are used to model disease transmission. The nodes represent individuals or populations, and the edges represent the probability or speed of infection. Researchers use these graphs to simulate outbreaks and to optimize strategies for controlling the spread of diseases, such as in COVID-19 contact tracing.

Social Network Graphs

Social networks such as Facebook, Instagram, and Twitter use weighted graphs to model user interactions. The weight of the edges between users can represent the strength of their relationship, such as the frequency of communication or the closeness of their relationship (e.g., close friends feature on Instagram). These graphs help platforms recommend new friends, posts, or content based on user’s behavior.

Network Packet Traffic Graphs

In cybersecurity, weighted graphs are used to analyze network traffic for threats such as malware or DDoS attacks. The nodes in the graph represent devices in a network, and the edges represent traffic flow, with weights indicating the volume or frequency of data packets. These graphs can help identify unusual traffic patterns, signaling potential breaches or network inefficiencies.

Programming Examples: Weighted Graph Implementation in Multiple Languages

Python Example: Dijkstra’s Algorithm

import heapq

def dijkstra(graph, start):
    distances = {node: float('infinity') for node in graph}
    distances[start] = 0
    pq = [(0, start)]

    while pq:
        current_distance, current_node = heapq.heappop(pq)

        if current_distance > distances[current_node]:
            continue

        for neighbor, weight in graph[current_node]:
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(pq, (distance, neighbor))

    return distances

graph = {
    'A': [('B', 1), ('C', 4)],
    'B': [('A', 1), ('C', 2), ('D', 5)],
    'C': [('A', 4), ('B', 2), ('D', 1)],
    'D': [('B', 5), ('C', 1)]
}

print(dijkstra(graph, 'A'))

Output:

{'A': 0, 'B': 1, 'C': 3, 'D': 4}

C++ Example: Dijkstra’s Algorithm

#include <iostream>
#include <vector>
#include <queue>
#include <limits>

using namespace std;

const int INF = numeric_limits<int>::max();

vector<int> dijkstra(const vector<vector<pair<int, int>>> &graph, int start) {
    vector<int> dist(graph.size(), INF);
    dist[start] = 0;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
    pq.push({0, start});

    while (!pq.empty()) {
        int current_dist = pq.top().first;
        int current_node = pq.top().second;
        pq.pop();

        if (current_dist > dist[current_node]) continue;

        for (const auto &neighbor : graph[current_node]) {
            int next_node = neighbor.first;
            int weight = neighbor.second;

            if (dist[current_node] + weight < dist[next_node]) {
                dist[next_node] = dist[current_node] + weight;
                pq.push({dist[next_node], next_node});
            }
        }
    }

    return dist;
}

int main() {
    vector<vector<pair<int, int>>> graph = {
        {{1, 1}, {2, 4}},
        {{0, 1}, {2, 2}, {3, 5}},
        {{0, 4}, {1, 2}, {3, 1}},
        {{1, 5}, {2, 1}}
    };

    vector<int> distances = dijkstra(graph, 0);

    for (int i = 0; i < distances.size(); i++) {
        cout << "Distance from node 0 to node " << i << " is " << distances[i] << endl;
    }

    return 0;
}

Output:

Distance from node 0 to node 0 is 0
Distance from node 0 to node 1 is 1
Distance from node 0 to node 2 is 3
Distance from node 0 to node 3 is 4

Advantages of Weighted Graphs

Better Representation of Real-World Scenarios: Weighted graphs allow for a more accurate representation of real-world situations. In applications such as road networks or telecommunication networks, weighted graphs capture varying degrees of importance or cost between connections.
Accurate Pathfinding: Algorithms such as Dijkstra’s or Bellman-Ford provide precise results when calculating the shortest path in weighted graphs, making them useful in transportation systems and logistics.
More Efficient Algorithms: Weighted graphs can be used with algorithms that optimize based on the additional information provided by edge weights. For example, Prim’s and Kruskal’s algorithms for minimum spanning trees are more efficient when used with weighted graphs.
Flexible Analysis: Weighted graphs offer a variety of analytical options, such as calculating the average weight of the edges or finding nodes with unusually high or low weights. This flexibility allows for advanced data analysis.
Modeling Uncertainty: Weighted graphs can model uncertain or probabilistic relationships between entities. This is useful in fields like machine learning, where probabilities between classes can be represented by edge weights.

Disadvantages of Weighted Graphs

Increased Complexity: Weighted graphs add an extra layer of complexity compared to unweighted graphs. This complexity can make it harder to implement, debug, and analyze algorithms.
Higher Memory Usage: Each edge in a weighted graph carries additional information (the weight), leading to higher memory requirements, which may be a limitation in memory-constrained environments.
More Difficult Maintenance: Changing the weights of edges can have cascading effects on the overall structure and behavior of a graph, making it harder to update and maintain.
Bias Towards Certain Properties: Weighted graphs can introduce biases based on the weights. For example, the shortest path algorithm always prefers the path with the least cost, which may not always be the most appropriate solution in some contexts.

Conclusion

Weighted graphs play a vital role in modeling a wide range of real-world scenarios, from optimizing transportation routes to handling complex dependencies in software development. While they offer several advantages such as better pathfinding and more accurate analysis, their complexity and memory demands present challenges that must be managed carefully.

With their broad range of applications—from artificial intelligence to epidemiology—weighted graphs remain a crucial part of many computational solutions today. Their versatility across domains and adaptability to a variety of problems ensure that they will continue to be a fundamental tool in fields that involve data structures, algorithms, and network analysis.

Video Credit: Nikhil Lohia

Frequently Asked Questions (FAQs) About Weighted Graphs

What is a Weighted Graph?

A weighted graph is a type of graph in which each edge is associated with a weight or cost. These weights can represent various values such as distance, cost, capacity, or any other measurement that quantifies the relationship between two nodes (also known as vertices). In an unweighted graph, every edge is treated equally, whereas in a weighted graph, the weights allow for a more nuanced understanding of the connections between nodes.

Real-World Example:

Imagine a road network where each intersection is a node, and the roads between them are the edges. The weight of each edge could represent the distance between two intersections, the time it takes to travel between them, or the fuel cost.

Example Code in Python (Weighted Graph using Adjacency List):

graph = {
    'A': [('B', 4), ('C', 3)],
    'B': [('A', 4), ('C', 1), ('D', 2)],
    'C': [('A', 3), ('B', 1), ('D', 4)],
    'D': [('B', 2), ('C', 4)]
}

print(graph)

Output:


'A': [('B', 4), ('C', 3)],
'B': [('A', 4), ('C', 1), ('D', 2)],
'C': [('A', 3), ('B', 1), ('D', 4)],
'D': [('B', 2), ('C', 4)]

How are Weighted Graphs Represented in Computer Memory?

Weighted graphs are commonly represented in two ways: adjacency matrices and adjacency lists.

Adjacency Matrix: This is a 2D array where each row and column represents a node. The value at the intersection of a row and column represents the weight of the edge between two nodes. If there’s no edge, the value is typically set to infinity or a large number.
Adjacency List: This is a more efficient representation, especially for sparse graphs. Each node has a list of its neighboring nodes along with the corresponding edge weights.

Example in C++ (Adjacency Matrix):

#include <iostream>
using namespace std;

int main() {
    int graph[4][4] = {
        {0, 4, 3, 0},
        {4, 0, 1, 2},
        {3, 1, 0, 4},
        {0, 2, 4, 0}
    };

    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            cout << graph[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

Output:

What Are Some Common Applications of Weighted Graphs?

Weighted graphs are used extensively in various fields due to their ability to model real-world systems. Common applications include:

Transportation Networks: In road networks, the weight on edges can represent the distance or travel time between locations. Algorithms such as Dijkstra’s and A* use weighted graphs to find the shortest path.
Telecommunication Networks: Here, the weights may represent the bandwidth or latency between two devices, allowing for the optimization of data flow.
AI and Decision Making: In AI game trees, the weights can represent the value of making certain decisions, guiding the algorithm to select the best action.
Supply Chain Management: In a network of suppliers and retailers, the weight might represent the cost of transporting goods between two locations.

How Does Dijkstra’s Algorithm Work on Weighted Graphs?

Dijkstra’s Algorithm is a popular algorithm used to find the shortest path between a starting node and all other nodes in a weighted graph. It works by maintaining a set of visited nodes and iteratively updating the shortest known distance from the start node to each node.

Python Implementation:

import heapq

def dijkstra(graph, start):
    distances = {node: float('infinity') for node in graph}
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)

        if current_distance > distances[current_node]:
            continue

        for neighbor, weight in graph[current_node]:
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances

graph = {
    'A': [('B', 1), ('C', 4)],
    'B': [('A', 1), ('C', 2), ('D', 5)],
    'C': [('A', 4), ('B', 2), ('D', 1)],
    'D': [('B', 5), ('C', 1)]
}

print(dijkstra(graph, 'A'))

Output:

{'A': 0, 'B': 1, 'C': 3, 'D': 4}

What is a Minimum Spanning Tree (MST) in a Weighted Graph?

A Minimum Spanning Tree (MST) is a subgraph of a weighted graph that connects all vertices with the minimum possible total edge weight and no cycles. It is particularly useful in network design where you want to minimize the cost of connecting different nodes (e.g., laying out cable or road networks).

Example of Prim’s Algorithm in C++:

#include <iostream>
#include <climits>
using namespace std;

#define V 5

int minKey(int key[], bool mstSet[]) {
    int min = INT_MAX, min_index;
    for (int v = 0; v < V; v++)
        if (!mstSet[v] && key[v] < min)
            min = key[v], min_index = v;
    return min_index;
}

void primMST(int graph[V][V]) {
    int parent[V];
    int key[V];
    bool mstSet[V];

    for (int i = 0; i < V; i++)
        key[i] = INT_MAX, mstSet[i] = false;

    key[0] = 0;
    parent[0] = -1;

    for (int count = 0; count < V - 1; count++) {
        int u = minKey(key, mstSet);
        mstSet[u] = true;

        for (int v = 0; v < V; v++)
            if (graph[u][v] && !mstSet[v] && graph[u][v] < key[v])
                parent[v] = u, key[v] = graph[u][v];
    }

    for (int i = 1; i < V; i++)
        cout << parent[i] << " - " << i << "  Weight: " << graph[i][parent[i]] << endl;
}

int main() {
    int graph[V][V] = {
        {0, 2, 0, 6, 0},
        {2, 0, 3, 8, 5},
        {0, 3, 0, 0, 7},
        {6, 8, 0, 0, 9},
        {0, 5, 7, 9, 0}
    };

    primMST(graph);
    return 0;
}

Output:

0 - 1  Weight: 2
1 - 2  Weight: 3
0 - 3  Weight: 6
1 - 4  Weight: 5

How is Kruskal’s Algorithm Different from Prim’s Algorithm in Finding MST?

Kruskal’s Algorithm and Prim’s Algorithm are both used to find the Minimum Spanning Tree (MST), but they operate differently:

Prim’s Algorithm grows the MST one vertex at a time by choosing the smallest edge that connects a vertex in the MST to a vertex outside the MST.
Kruskal’s Algorithm focuses on edges, choosing the smallest edge that does not form a cycle and gradually adding them to the MST.

Kruskal’s Algorithm in Java:

import java.util.*;

class Edge implements Comparable<Edge> {
    int src, dest, weight;

    public int compareTo(Edge compareEdge) {
        return this.weight - compareEdge.weight;
    }
}

class Subset {
    int parent, rank;
}

public class Kruskal {
    int V, E

;
    Edge edge[];

    Kruskal(int v, int e) {
        V = v;
        E = e;
        edge = new Edge[E];
        for (int i = 0; i < e; ++i)
            edge[i] = new Edge();
    }

    int find(Subset subsets[], int i) {
        if (subsets[i].parent != i)
            subsets[i].parent = find(subsets, subsets[i].parent);
        return subsets[i].parent;
    }

    void Union(Subset subsets[], int x, int y) {
        int xroot = find(subsets, x);
        int yroot = find(subsets, y);
        if (subsets[xroot].rank < subsets[yroot].rank)
            subsets[xroot].parent = yroot;
        else if (subsets[xroot].rank > subsets[yroot].rank)
            subsets[yroot].parent = xroot;
        else {
            subsets[yroot].parent = xroot;
            subsets[xroot].rank++;
        }
    }

    void KruskalMST() {
        Edge result[] = new Edge[V];
        int e = 0;
        int i = 0;
        for (i = 0; i < V; ++i)
            result[i] = new Edge();

        Arrays.sort(edge);
        Subset subsets[] = new Subset[V];
        for (i = 0; i < V; ++i)
            subsets[i] = new Subset();
        for (int v = 0; v < V; ++v) {
            subsets[v].parent = v;
            subsets[v].rank = 0;
        }

        i = 0;
        while (e < V - 1) {
            Edge next_edge = edge[i++];
            int x = find(subsets, next_edge.src);
            int y = find(subsets, next_edge.dest);
            if (x != y) {
                result[e++] = next_edge;
                Union(subsets, x, y);
            }
        }

        System.out.println("Following are the edges in the constructed MST");
        for (i = 0; i < e; ++i)
            System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);
    }

    public static void main(String[] args) {
        int V = 4; 
        int E = 5; 
        Kruskal graph = new Kruskal(V, E);
        graph.edge[0].src = 0;
        graph.edge[0].dest = 1;
        graph.edge[0].weight = 10;
        graph.edge[1].src = 0;
        graph.edge[1].dest = 2;
        graph.edge[1].weight = 6;
        graph.edge[2].src = 0;
        graph.edge[2].dest = 3;
        graph.edge[2].weight = 5;
        graph.edge[3].src = 1;
        graph.edge[3].dest = 3;
        graph.edge[3].weight = 15;
        graph.edge[4].src = 2;
        graph.edge[4].dest = 3;
        graph.edge[4].weight = 4;

        graph.KruskalMST();
    }
}

Output:

Following are the edges in the constructed MST:
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10

How are Weighted Graphs Used in AI and Decision-Making?

In Artificial Intelligence (AI), weighted graphs can be used to model decision trees where each node represents a decision, and the weight of each edge represents the “cost” or “utility” of making a particular decision. This is often seen in games (e.g., chess or checkers), where each move has a specific weight depending on its strategic advantage.

For example, in a game of tic-tac-toe, each move can be assigned a weight based on how close it brings a player to victory. In AI algorithms such as minimax or expectimax, the graph of possible moves and their outcomes is analyzed to select the best move.

Can Weighted Graphs Be Used in Image Processing?

Yes, weighted graphs are used in image processing, particularly in tasks like image segmentation. Each pixel in the image can be represented as a node, and the edges between pixels are weighted based on their similarity (e.g., color difference, brightness). Algorithms such as graph cuts are then used to partition the image into different segments by minimizing the total weight of the edges that are “cut” to separate the nodes.

Example in Python Using OpenCV:

import cv2
import numpy as np

image = cv2.imread('image.jpg', 0)
edges = cv2.Canny(image, 100, 200)

cv2.imshow('Edges', edges)
cv2.waitKey(0)
cv2.destroyAllWindows()

How Are Weighted Graphs Used in Network Packet Traffic Analysis?

In network security and packet traffic analysis, weighted graphs can model the flow of data packets between different network nodes. The weight of an edge might represent the bandwidth or the delay between two nodes. This is useful for detecting anomalies in traffic patterns, such as distributed denial-of-service (DDoS) attacks, where certain edges may suddenly experience a spike in traffic, indicated by an increased weight.

Network security tools often use these graphs to track traffic over time and provide insights for optimizing data flow or detecting malicious activities.

How Do Weighted Graphs Help in Social Network Analysis?

Social networks can also be modeled as weighted graphs, where the nodes represent users, and the edges represent relationships between them. The weight of an edge could represent the strength of a relationship (e.g., frequency of interactions). For instance, Facebook or Instagram can use weighted graphs to recommend “close friends” based on the intensity of your interactions with certain users, such as likes, messages, and comments.

In graph-based machine learning, these weights can serve as inputs for algorithms that detect communities within the social network.

How Can I Implement Bellman-Ford Algorithm for Weighted Graphs?

The Bellman-Ford algorithm is another shortest path algorithm that works on graphs with negative weights, unlike Dijkstra’s algorithm. It computes the shortest path from a single source to all other vertices.

Example in Python:

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = []

    def add_edge(self, u, v, w):
        self.graph.append([u, v, w])

    def bellman_ford(self, src):
        dist = [float("inf")] * self.V
        dist[src] = 0

        for _ in range(self.V - 1):
            for u, v, w in self.graph:
                if dist[u] != float("inf") and dist[u] + w < dist[v]:
                    dist[v] = dist[u] + w

        for u, v, w in self.graph:
            if dist[u] != float("inf") and dist[u] + w < dist[v]:
                print("Graph contains negative weight cycle")
                return

        self.print_solution(dist)

    def print_solution(self, dist):
        print("Vertex Distance from Source")
        for i in range(self.V):
            print("{0}\t\t{1}".format(i, dist[i]))

g = Graph(5)
g.add_edge(0, 1, -1)
g.add_edge(0, 2, 4)
g.add_edge(1, 2, 3)
g.add_edge(1, 3, 2)
g.add_edge(1, 4, 2)
g.add_edge(3, 2, 5)
g.add_edge(3, 1, 1)
g.add_edge(4, 3, -3)

g.bellman_ford(0)

Output:

Vertex Distance from Source
0       0
1       -1
2       2
3       -2
4       1

How Are Weighted Graphs Used in Compilers?

In compilers, weighted graphs are used extensively in optimization tasks such as data-flow analysis and type inference. For example, in a control flow graph (CFG), the nodes represent blocks of code, and the edges represent the control flow between them. The weight of an edge might represent the execution cost of moving from one block to another.

This allows the compiler to optimize code by identifying “hot paths” that are frequently executed and applying optimizations like loop unrolling or inlining.

How Are Weighted Graphs Used in Natural Language Processing (NLP)?

In Natural Language Processing (NLP), weighted graphs are used in various applications such as text classification and semantic analysis. For instance, in a word co-occurrence graph, each word in a document is represented as a node, and the edges between nodes represent how frequently the words co-occur. The weight of an edge could represent the frequency or significance of this co-occurrence.

Weighted graphs can also be used for topic modeling, where the edges represent the similarity between different topics based on the terms they share.

How Are Weighted Graphs Used in Image Segmentation?

In image segmentation, weighted graphs help partition an image into different regions. Each pixel is represented as a node, and the edge weights between pixels represent their similarity. Graph cuts algorithms are used to find the optimal partitioning of the image into distinct regions, minimizing the sum of the weights of the edges that are cut.

Can Weighted Graphs Represent Probabilistic Relationships?

Yes, weighted graphs can represent probabilistic relationships. In such graphs, the weight of an edge can denote the probability of a particular connection or transition occurring between nodes. This is useful in Bayesian Networks and Hidden Markov Models, where the weights represent conditional probabilities or transition probabilities between states.

How Are Weighted Graphs Used in Document Link Analysis?

In document link analysis, weighted graphs can model the links between web pages or documents. The nodes represent web pages, and the edges represent hyperlinks. The weight of an edge could represent the number of links, page rank, or some other measure of relevance or authority.

Google PageRank is an example of an algorithm that uses weighted graphs to rank web pages based on their link structure.

Example in Python:

import numpy as np

def page_rank(M, num_iterations: int, d: float):
    M = np.array(M)
    N = M.shape[1]
    v = np.random.rand(N, 1)
    v = v / np.linalg.norm(v, 1)

    M = M / M.sum(axis=0)
    M = d * M + (1 - d) / N

    for i in range(num_iterations):
        v = np.dot(M, v)

    return v

M = [
    [0, 0.5, 0],
    [0.5, 0, 0.5],
    [0.5, 0.5, 0.5]
]

print(page_rank(M, 100, 0.85))

Output:

[[0.19166667]
 [0.33333333]
 [0.475     ]]

What Are Some Practical Challenges in Working with Weighted Graphs?

When working with weighted graphs, several practical challenges may arise:

Complexity: Weighted graphs can be more complex to work with compared to unweighted graphs. The additional information (weights) makes algorithms more complicated.
Memory Usage: Storing weights for every edge can increase memory consumption, especially in large graphs.
Maintenance: Updating weights can be challenging, especially if changes affect the entire structure or if there are constraints on how updates are handled.
Bias: Algorithms may introduce biases based on edge weights, which can affect the outcomes and insights derived from the graph.

How Are Weighted Graphs Used in Epidemic Modeling?

Epidemic modeling can use weighted graphs to represent the spread of diseases. Nodes in the graph represent individuals, and edges represent possible transmission paths between them. The weight of an edge might represent the probability of disease transmission between two individuals or the time it takes for the disease to spread.

SIR models and other epidemiological models can leverage these weighted graphs to simulate and predict the spread of infectious diseases.

Can Weighted Graphs Be Used in Quantum Field Theory?

In quantum field theory, weighted graphs can represent the states of a quantum system and the transitions between them. The vertices of the graph represent quantum states, and the edges represent possible transitions, with weights corresponding to the amplitude of these transitions. This can help analyze path integrals and quantum amplitudes, providing insights into the behavior of quantum systems.

How Are Weighted Graphs Utilized in Scheduling and Optimization?

In scheduling and optimization, weighted graphs can model various constraints and objectives. For example, in project scheduling, nodes might represent tasks, and edges might represent dependencies between tasks with weights representing the cost or time required to complete each task. Critical Path Method (CPM) and Program Evaluation and Review Technique (PERT) are examples of techniques that utilize weighted graphs to optimize project schedules.

Example in Python (Job Scheduling):

import networkx as nx

G = nx.DiGraph()
G.add_edge('A', 'B', weight=3)
G.add_edge('A', 'C', weight=4)
G.add_edge('B', 'D', weight=2)
G.add_edge('C', 'D', weight=1)

lengths = nx.single_source_dijkstra_path_length(G, 'A')
print(lengths)

Output:

{'A': 0, 'B': 3, 'C': 4, 'D': 4}

Understanding Weighted Graphs: A Comprehensive Exploration

What is a Weighted Graph?

Table of Contents

Applications of Weighted Graphs

2D Matrix Games

Spanning Trees

Constraint Graphs

Dependency Graphs

Compilers

Artificial Intelligence

Image Processing

Natural Language Processing

Real-World Applications of Weighted Graphs

Transportation Networks

Document Link Graphs

Epidemiology

Social Network Graphs

Network Packet Traffic Graphs

Programming Examples: Weighted Graph Implementation in Multiple Languages

Python Example: Dijkstra’s Algorithm

C++ Example: Dijkstra’s Algorithm

Advantages of Weighted Graphs

Disadvantages of Weighted Graphs

Conclusion

Related Articles

Read More Articles

Frequently Asked Questions (FAQs) About Weighted Graphs

What is a Weighted Graph?

Real-World Example:

Example Code in Python (Weighted Graph using Adjacency List):

Output:

How are Weighted Graphs Represented in Computer Memory?

Example in C++ (Adjacency Matrix):

Output:

What Are Some Common Applications of Weighted Graphs?

How Does Dijkstra’s Algorithm Work on Weighted Graphs?

Python Implementation:

Output:

What is a Minimum Spanning Tree (MST) in a Weighted Graph?

Example of Prim’s Algorithm in C++:

Output:

How is Kruskal’s Algorithm Different from Prim’s Algorithm in Finding MST?

Kruskal’s Algorithm in Java:

Output:

How are Weighted Graphs Used in AI and Decision-Making?

Can Weighted Graphs Be Used in Image Processing?

Example in Python Using OpenCV:

How Are Weighted Graphs Used in Network Packet Traffic Analysis?

How Do Weighted Graphs Help in Social Network Analysis?

How Can I Implement Bellman-Ford Algorithm for Weighted Graphs?

Example in Python:

Output:

How Are Weighted Graphs Used in Compilers?

How Are Weighted Graphs Used in Natural Language Processing (NLP)?

How Are Weighted Graphs Used in Image Segmentation?

Can Weighted Graphs Represent Probabilistic Relationships?

How Are Weighted Graphs Used in Document Link Analysis?

Example in Python:

What Are Some Practical Challenges in Working with Weighted Graphs?

How Are Weighted Graphs Used in Epidemic Modeling?

Can Weighted Graphs Be Used in Quantum Field Theory?

How Are Weighted Graphs Utilized in Scheduling and Optimization?

Example in Python (Job Scheduling):

Output: