Understanding Trie Data Structure In Depth: A Comprehensive Guide

In the world of data structures, where speed and efficiency are paramount, Trie (pronounced as “try”) stands out as a powerful solution, particularly when dealing with string-related operations like searching, insertion, and prefix matching. Derived from the word “retrieval,” a Trie is a tree-based data structure that stores strings efficiently, making operations like auto-completion and spell-checking fast and scalable. In this detailed article, we will explore the Trie data structure, its various operations, advantages, disadvantages, and real-world applications.

What is a Trie Data Structure?

A Trie, also known as a prefix tree or digital tree, is a specialized tree data structure used for storing a set of strings, where the position of each node represents a single character in a string. It is commonly used to handle prefix-based operations like searching, insertion, and deletion of strings.

The structure of a Trie is quite different from other tree-based data structures. Instead of storing the entire string in a node, each node represents a character of the string. By traversing the Trie, we can reconstruct the entire word. The key idea behind a Trie is that it breaks down strings into their individual characters and uses the tree structure to connect nodes, based on their character sequence.

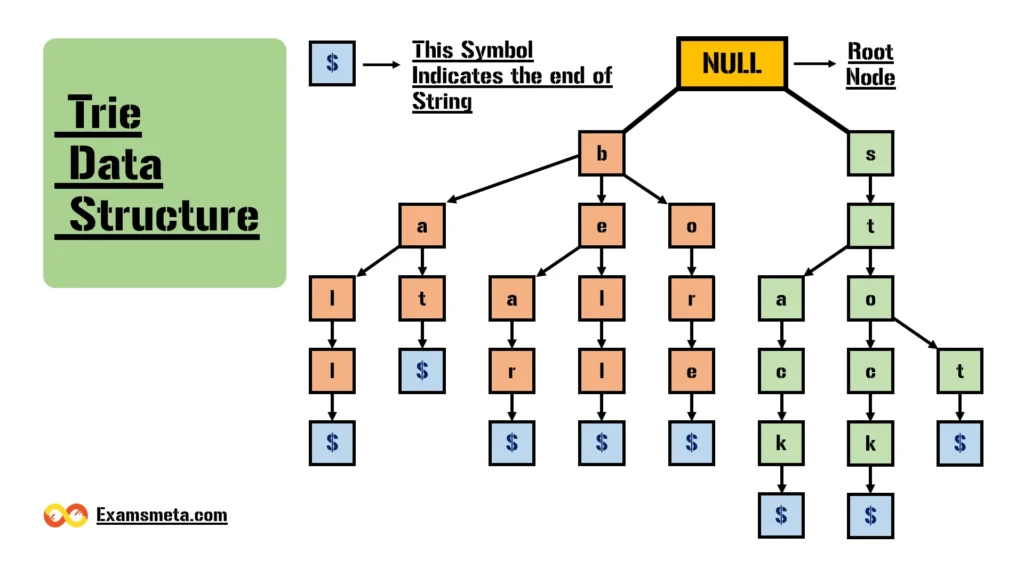
Key Properties of a Trie

Root Node: The root node of the Trie is a null node (i.e., it doesn’t store any character).
Children Nodes: Each node can have a maximum of 26 children (assuming we’re using the English alphabet with 26 letters). Each child corresponds to one character.
Alphabetical Order: The children of each node are sorted alphabetically.
Depth: The depth of the Trie is determined by the length of the longest word inserted.
End of Word: A flag is used at the end of each word to indicate that a complete word exists at that node.

For example, let’s consider the following set of words: bear, bell, bat, bore, ball, stop, stock, stack. The Trie structure for these words would have nodes branching out based on the characters in each word, with shared prefixes (like “b” in bat and ball) creating fewer nodes for those prefixes.

Why Use a Trie?

The main advantage of a Trie over other data structures (like hash tables or binary search trees) is its ability to efficiently handle large sets of strings, especially when prefix-based searching is required. This makes Trie a good choice for applications like auto-complete and spell-check. In such cases, the search space can be drastically reduced by quickly identifying the prefix of the input string and then searching only among the nodes under that prefix.

Basic Operations of a Trie

In a Trie, we can perform three basic operations:

Insertion of a Node
Searching for a Node
Deletion of a Node

We will cover each operation in detail, along with code implementations and explanations for each step.

1. Insertion of a Node in a Trie

The process of inserting a word into a Trie is fairly straightforward. Each letter of the word is inserted individually as a new node, if it doesn’t already exist at that position in the Trie. Here’s how insertion works:

Step 1: Start from the root node.
Step 2: For each character in the word, check if there is an existing node for that character at the current level of the Trie.
Step 3: If the node exists, move to the child node. Otherwise, create a new node for that character.
Step 4: After inserting the last character, mark the node as the end of a word.

Here is the Java implementation of inserting a node into a Trie:

public class Data_Trie {  
    private Node_Trie root;  

    public Data_Trie() {  
        this.root = new Node_Trie();  
    }  

    public void insert(String word) {  
        Node_Trie current = root;  
        int length = word.length();  
        for (int x = 0; x < length; x++) {  
            char L = word.charAt(x);  
            Node_Trie node = current.getNode().get(L);  
            if (node == null) {  
                node = new Node_Trie ();  
                current.getNode().put(L, node);  
            }  
            current = node;  
        }  
        current.setWord(true);  
    }  
}

Explanation of Code:

Data_Trie Class: This class defines the Trie data structure. It has a root node that is initialized in the constructor.
insert Method: This method inserts a word into the Trie. For each character of the word, it either moves to the child node if it already exists or creates a new node if it doesn’t.
current.setWord(true): This marks the node as the end of a word once all characters have been inserted.

2. Searching for a Node in a Trie

Searching for a word in a Trie is quite similar to insertion, but instead of creating new nodes, we traverse the existing nodes based on the characters of the input word. If we can follow the entire path of the word in the Trie and reach a node marked as the end of a word, the word exists in the Trie.

Here is the Java implementation of searching a word in the Trie:

class Search_Trie {  
    private Node_Trie Prefix_Search(String W) {  
        Node_Trie node = R;  
        for (int x = 0; x < W.length(); x++) {  
           char curLetter = W.charAt(x);  
           if (node.containsKey(curLetter)) {  
               node = node.get(curLetter);  
           } else {  
               return null;  
           }  
        }  
        return node;  
    }  

    public boolean search(String W) {  
       Node_Trie node = Prefix_Search(W);  
       return node != null && node.isEnd();  
    }  
}

Explanation of Code:

Prefix_Search Method: This helper method traverses the Trie based on the input word and returns the last node if the word exists in the Trie.
search Method: This method uses Prefix_Search to check if the word exists. If the word exists, it returns true; otherwise, false.

3. Deletion of a Node in a Trie

Deletion in a Trie is more complex than insertion and searching because we need to ensure that we don’t remove nodes that are part of other words. Here’s the logic:

Step 1: Start from the root node and follow the path of the word.
Step 2: If the word exists, mark the last node as not being the end of a word.
Step 3: If the node has no other children and is not part of another word, delete the node.
Step 4: Recursively delete unused nodes.

Here is the Java implementation of deleting a word from a Trie:

public void Node_delete(String W) {  
    Node_delete(R, W, 0);  
}  

private boolean Node_delete(Node_Trie current, String W, int Node_index) {  
    if (Node_index == W.length()) {  
        if (!current.isEndOfWord()) {  
            return false;  
        }  
        current.setEndOfWord(false);  
        return current.getChildren().isEmpty();  
    }  
    char A = W.charAt(Node_index);  
    Node_Trie node = current.getChildren().get(A);  
    if (node == null) {  
        return false;  
    }  
    boolean Current_Node_Delete = Node_delete(node, W, Node_index + 1) && !node.isEndOfWord();  

    if (Current_Node_Delete) {  
        current.getChildren().remove(A);  
        return current.getChildren().isEmpty();  
    }  
    return false;  
}

Explanation of Code:

Node_delete Method: This method recursively deletes a word from the Trie, ensuring that nodes are only removed if they are no longer needed.
isEndOfWord(): This checks whether the current node is marked as the end of a word. If it is not, we can safely delete the node.

Real-World Applications of Trie

Spell Checker:
A Trie can store a dictionary of valid words. When a word is entered, the Trie can quickly check for its presence and suggest valid alternatives based on common prefixes.
Auto-Complete:
By storing frequently used words in a Trie, an auto-complete system can provide word suggestions based on the characters typed by a user. This is often used in search engines, IDEs, and mobile keyboards.
URL Matching:
Web browsers use Tries to match URLs based on user input. As a user types, the Trie can suggest previously visited URLs that match the input.

Advantages of Trie

Fast Searching: Unlike hash tables or binary search trees, Trie can search for words efficiently, especially when dealing with prefixes.
Efficient Storage of Strings: Since nodes can be shared among words with common prefixes, Trie reduces memory consumption compared to other data structures.

Disadvantages of Trie

Memory Usage: Trie can consume more memory because it requires multiple nodes, each representing a single character.
Slower Than Hash Tables: For exact string matching, hash tables are usually faster than Trie. However, for prefix-based searches, Trie is more efficient.

Implementation of Trie Data Structure In Java Programming Language

Here’s the corrected and properly implemented Trie data structure with insertion, searching, and deletion operations in Java. The key points are explained step-by-step, followed by the Node_Trie class and main function to demonstrate the usage.

Code:

import java.util.HashMap;
import java.util.Map;

class Node_Trie {
    char value;
    Map<Character, Node_Trie> children;
    boolean isEndOfWord;

    public Node_Trie(char value) {
        this.value = value;
        this.children = new HashMap<>();
        this.isEndOfWord = false;
    }
}

public class Trie {
    private Node_Trie root;

    public Trie() {
        root = new Node_Trie('\0');  // Root node is initialized with null character.
    }

    // Insertion method
    public void insert(String word) {
        Node_Trie current = root;
        for (char ch : word.toCharArray()) {
            current.children.putIfAbsent(ch, new Node_Trie(ch));
            current = current.children.get(ch);
        }
        current.isEndOfWord = true;
    }

    // Searching method
    public boolean search(String word) {
        Node_Trie current = root;
        for (char ch : word.toCharArray()) {
            current = current.children.get(ch);
            if (current == null) {
                return false;
            }
        }
        return current.isEndOfWord;
    }

    // Deletion method
    public void delete(String word) {
        deleteHelper(root, word, 0);
    }

    private boolean deleteHelper(Node_Trie current, String word, int index) {
        if (index == word.length()) {
            if (!current.isEndOfWord) {
                return false; // Word not found.
            }
            current.isEndOfWord = false;
            return current.children.isEmpty(); // If no other children, node can be deleted.
        }
        char ch = word.charAt(index);
        Node_Trie node = current.children.get(ch);
        if (node == null) {
            return false; // Word not found.
        }
        boolean shouldDeleteCurrentNode = deleteHelper(node, word, index + 1);

        if (shouldDeleteCurrentNode) {
            current.children.remove(ch);
            return current.children.isEmpty() && !current.isEndOfWord;
        }
        return false;
    }

    // Print all words in the Trie
    public void printTrie() {
        printTrieHelper(root, new StringBuilder());
    }

    private void printTrieHelper(Node_Trie current, StringBuilder prefix) {
        if (current.isEndOfWord) {
            System.out.println(prefix.toString());
        }
        for (char ch : current.children.keySet()) {
            prefix.append(ch);
            printTrieHelper(current.children.get(ch), prefix);
            prefix.deleteCharAt(prefix.length() - 1);
        }
    }

    public static void main(String[] args) {
        Trie trie = new Trie();

        // Inserting words into the Trie
        trie.insert("oh");
        trie.insert("way");
        trie.insert("bag");
        trie.insert("can");

        // Searching for words
        System.out.println("Search 'oh': " + trie.search("oh"));
        System.out.println("Search 'bag': " + trie.search("bag"));
        System.out.println("Search 'can': " + trie.search("can"));
        System.out.println("Search 'ways': " + trie.search("ways"));
        System.out.println("Search 'way': " + trie.search("way"));

        // Printing the Trie
        System.out.println("Current Trie:");
        trie.printTrie();

        // Deleting words
        trie.delete("oh");
        System.out.println("Deleting 'oh'...\nCurrent Trie:");
        trie.printTrie();

        trie.delete("can");
        System.out.println("Deleting 'can'...\nCurrent Trie:");
        trie.printTrie();
    }
}

Explanation of Key Steps:

Node_Trie Class:
- This class represents the structure of a Trie node. Each node contains:
  - char value: The character stored at this node.
  - Map<Character, Node_Trie> children: A HashMap is used to store child nodes, allowing quick access to the next character in the word.
  - boolean isEndOfWord: A flag indicating if this node represents the end of a word.
Trie Class:
- The Trie class manages the root node and implements the operations for insertion, searching, and deletion.
  - insert Method:
    - This method takes a word as input and traverses through the Trie, adding a node for each character in the word if it does not exist.
    - The final node is marked as the end of the word by setting isEndOfWord = true.
  - search Method:
    - It traverses through the Trie using each character in the word.
    - If the traversal reaches the end of the word and isEndOfWord is true, the word exists in the Trie.
  - delete Method:
    - This method deletes a word from the Trie using a recursive helper function (deleteHelper).
    - If the node can be safely deleted (i.e., it has no children and is not the end of any other word), the function removes the node from its parent.
  - printTrie Method:
    - Recursively prints all the words stored in the Trie by traversing each node and concatenating the characters.

Sample Output:

Search 'oh': true
Search 'bag': true
Search 'can': true
Search 'ways': false
Search 'way': true
Current Trie:
bag
can
oh
way
Deleting 'oh'...
Current Trie:
bag
can
way
Deleting 'can'...
Current Trie:
bag
way

Explanation of Output:

The insert operation adds words like "oh", "way", "bag", and "can" to the Trie.
The search operation successfully finds "oh", "bag", "can", and "way", but fails to find "ways".
The delete operation removes "oh" and "can" from the Trie. After deletion, the Trie only contains "bag" and "way".

This demonstrates how the Trie efficiently handles insertion, searching, and deletion of strings, while preserving the structure of the remaining words.

Implementation of Trie Data Structure In C++ Programming Language

Here is a C++ implementation of the Trie data structure with insertion, searching, and deletion operations. An explanation for each step is also provided to describe how these operations are applied.

C++ Code Implementation:

#include <iostream>
#include <unordered_map>
using namespace std;

// Node_Trie class represents each node in the Trie
class Node_Trie {
public:
    char value;                                // Character stored in the node
    unordered_map<char, Node_Trie*> children;   // Hash map to store child nodes
    bool isEndOfWord;                          // Flag to indicate end of word

    // Constructor for Node_Trie
    Node_Trie(char value) {
        this->value = value;
        this->isEndOfWord = false;
    }
};

// Trie class to manage root and operations
class Trie {
private:
    Node_Trie* root;

public:
    // Constructor initializes root node
    Trie() {
        root = new Node_Trie('\0');  // Root initialized with null character
    }

    // Insert method for adding words to Trie
    void insert(string word) {
        Node_Trie* current = root;
        for (char ch : word) {
            // If child node does not exist, create one
            if (current->children.find(ch) == current->children.end()) {
                current->children[ch] = new Node_Trie(ch);
            }
            current = current->children[ch];
        }
        current->isEndOfWord = true;  // Mark the end of the word
    }

    // Search method to check if a word exists in the Trie
    bool search(string word) {
        Node_Trie* current = root;
        for (char ch : word) {
            if (current->children.find(ch) == current->children.end()) {
                return false;  // Word not found
            }
            current = current->children[ch];
        }
        return current->isEndOfWord;  // Return true if it's the end of a valid word
    }

    // Helper function for deleting a word from the Trie
    bool deleteHelper(Node_Trie* current, string word, int index) {
        if (index == word.length()) {
            // When end of the word is reached
            if (!current->isEndOfWord) {
                return false;  // Word not found
            }
            current->isEndOfWord = false;
            return current->children.empty();  // If node has no children, it can be deleted
        }

        char ch = word[index];
        Node_Trie* node = current->children[ch];
        if (node == nullptr) {
            return false;  // Word not found
        }

        bool shouldDeleteCurrentNode = deleteHelper(node, word, index + 1);

        // If true, delete the mapping of character and node
        if (shouldDeleteCurrentNode) {
            current->children.erase(ch);
            return current->children.empty() && !current->isEndOfWord;
        }

        return false;
    }

    // Public method to delete a word
    void deleteWord(string word) {
        deleteHelper(root, word, 0);
    }

    // Helper function to print the Trie
    void printTrieHelper(Node_Trie* current, string word) {
        if (current->isEndOfWord) {
            cout << word << endl;
        }
        for (auto child : current->children) {
            printTrieHelper(child.second, word + child.first);
        }
    }

    // Public method to print all words in the Trie
    void printTrie() {
        printTrieHelper(root, "");
    }
};

int main() {
    Trie trie;

    // Insert words into Trie
    trie.insert("apple");
    trie.insert("app");
    trie.insert("bat");
    trie.insert("ball");

    // Searching words in Trie
    cout << "Search for 'app': " << (trie.search("app") ? "Found" : "Not Found") << endl;
    cout << "Search for 'apple': " << (trie.search("apple") ? "Found" : "Not Found") << endl;
    cout << "Search for 'bat': " << (trie.search("bat") ? "Found" : "Not Found") << endl;
    cout << "Search for 'ball': " << (trie.search("ball") ? "Found" : "Not Found") << endl;
    cout << "Search for 'batman': " << (trie.search("batman") ? "Found" : "Not Found") << endl;

    // Printing all words in the Trie
    cout << "\nCurrent words in Trie:" << endl;
    trie.printTrie();

    // Deleting words from Trie
    trie.deleteWord("apple");
    cout << "\nDeleting 'apple'...\n";
    trie.printTrie();

    trie.deleteWord("bat");
    cout << "\nDeleting 'bat'...\n";
    trie.printTrie();

    return 0;
}

Explanation of Key Steps:

1. Node_Trie Class:

Purpose: Represents each node in the Trie. Each node stores:
char value: The character that this node represents.
unordered_map<char, Node_Trie*> children: Stores the child nodes (characters) in a hash map, making it easy to access child nodes.
bool isEndOfWord: A flag that indicates if this node marks the end of a valid word.

2. Trie Class:

insert Method:
- Steps:
  - The method takes a string as input.
  - It starts at the root and iterates over each character in the string.
  - For each character, it checks whether the corresponding child node exists in the children map. If not, it creates a new node.
  - Moves down the Trie as each character is added, marking the final node as the end of the word.
- Example:
  - Insert "apple". Nodes will be created for each character: 'a', 'p', 'p', 'l', 'e', and the node 'e' will be marked as the end of the word.
search Method:
- Steps:
  - Takes a string as input and traverses the Trie node by node using the characters in the string.
  - If at any point a character node is missing, the word is not present in the Trie.
  - If it successfully reaches the last character and finds that it marks the end of a word, it returns true; otherwise, false.
- Example:
  - Search for "app": If all the nodes corresponding to 'a', 'p', and 'p' exist and the 'p' node is marked as the end of a word, it returns true.
deleteWord Method:
- Steps:
  - The deleteHelper function recursively traverses the Trie to remove a word.
  - It deletes the nodes in reverse order if they are no longer needed (i.e., they are not part of another word).
  - If a node is found to be the end of a word, the flag is unset, and further deletion depends on whether that node has any children.
- Example:
  - Delete "apple": The nodes corresponding to 'l' and 'e' will be deleted if no other word shares this path. The node 'p' may remain if it is part of another word, such as "app".
printTrie Method:
- Steps:
  - Recursively prints all the words stored in the Trie.
  - Starts from the root and follows each character’s path to print complete words.
- Example:
  - The Trie contains the words "app", "apple", "bat", and "ball". After deletion, it may print only "app" and "ball".

Sample Output:

Search for 'app': Found
Search for 'apple': Found
Search for 'bat': Found
Search for 'ball': Found
Search for 'batman': Not Found

Current words in Trie:
app
apple
ball
bat

Deleting 'apple'...

Current words in Trie:
app
ball
bat

Deleting 'bat'...

Current words in Trie:
app
ball

Explanation of Output:

The insert operation successfully adds "app", "apple", "bat", and "ball" to the Trie.
The search operation correctly finds "app", "apple", "bat", and "ball", but it does not find "batman" because it was never inserted.
The delete operation removes "apple" and "bat" from the Trie, leaving only "app" and "ball" in the Trie.

Implementation of Trie Data Structure In Python Programming Language

Here is a Python implementation of the Trie data structure with insertion, searching, and deletion operations. I have provided a detailed explanation of each step in the code to describe how the operations are applied.

Python Code Implementation:

class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_end_of_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

    # Insert a word into the Trie
    def insert(self, word):
        current_node = self.root
        for char in word:
            if char not in current_node.children:
                current_node.children[char] = TrieNode()  # Create new node if character is missing
            current_node = current_node.children[char]
        current_node.is_end_of_word = True  # Mark the end of the word

    # Search for a word in the Trie
    def search(self, word):
        current_node = self.root
        for char in word:
            if char not in current_node.children:
                return False  # If character is not found, word does not exist
            current_node = current_node.children[char]
        return current_node.is_end_of_word  # Return True only if it's the end of a valid word

    # Helper function for deletion
    def _delete(self, current_node, word, index):
        if index == len(word):
            # If end of the word is reached
            if not current_node.is_end_of_word:
                return False  # Word does not exist in the Trie
            current_node.is_end_of_word = False
            return len(current_node.children) == 0  # If no children, node can be deleted

        char = word[index]
        if char not in current_node.children:
            return False  # Word does not exist in the Trie

        # Recurse to the next character
        can_delete_node = self._delete(current_node.children[char], word, index + 1)

        # If True, delete the current node's reference to the character
        if can_delete_node:
            del current_node.children[char]
            return len(current_node.children) == 0  # Return True if no more children

        return False

    # Public function to delete a word from the Trie
    def delete(self, word):
        self._delete(self.root, word, 0)

    # Print all words in the Trie
    def print_trie(self):
        def _print_trie(current_node, current_word):
            if current_node.is_end_of_word:
                print(current_word)
            for char, next_node in current_node.children.items():
                _print_trie(next_node, current_word + char)

        _print_trie(self.root, "")

# Main program to test the Trie
if __name__ == "__main__":
    trie = Trie()

    # Insert words
    trie.insert("cat")
    trie.insert("car")
    trie.insert("bat")
    trie.insert("ball")

    # Search words
    print("Search Results:")
    print(f"Is 'cat' in the Trie? {'Yes' if trie.search('cat') else 'No'}")
    print(f"Is 'car' in the Trie? {'Yes' if trie.search('car') else 'No'}")
    print(f"Is 'bat' in the Trie? {'Yes' if trie.search('bat') else 'No'}")
    print(f"Is 'ball' in the Trie? {'Yes' if trie.search('ball') else 'No'}")
    print(f"Is 'cow' in the Trie? {'Yes' if trie.search('cow') else 'No'}")

    # Print all words in the Trie
    print("\nWords in Trie:")
    trie.print_trie()

    # Delete words and show the results
    trie.delete("car")
    print("\nAfter deleting 'car':")
    trie.print_trie()

    trie.delete("bat")
    print("\nAfter deleting 'bat':")
    trie.print_trie()

Explanation of Key Steps:

1. TrieNode Class:

Purpose: Each node in the Trie represents a single character in a word.
children: A dictionary that holds references to child nodes. Each key is a character, and the value is a TrieNode object.
is_end_of_word: A boolean flag that is True when the node marks the end of a valid word.

2. Trie Class:

The Trie is built using the TrieNode objects. The class provides methods to insert, search, delete, and print words in the Trie.

3. Insert Method:

Steps:
- The insert method takes a word as input and iterates over each character.
- For each character, it checks if it exists in the current node’s children. If not, it creates a new node.
- Once all characters are added, the node representing the last character is marked as the end of the word.
Example:
- Insert "cat": Nodes will be created for 'c', 'a', and 't'. The node for 't' will be marked as the end of the word.

4. Search Method:

Steps:
- The search method takes a word as input and traverses the Trie node by node using the characters in the word.
- If a character is not found, it returns False.
- If it successfully reaches the last character and the node is marked as the end of the word, it returns True.
Example:
- Search for "cat": If the nodes corresponding to 'c', 'a', and 't' exist and the node for 't' is marked as the end of the word, it returns True.

5. Delete Method:

Steps:
- The delete method uses the helper function _delete, which works recursively to remove a word.
- It checks if a node can be deleted by determining if it has any child nodes and whether it marks the end of another word.
- If it finds that a node has no children and is not the end of another word, it deletes the node.
Example:
- Delete "car": The nodes for 'c', 'a', and 'r' will be removed if no other word shares this path.

6. print_trie Method:

Steps:
- This method recursively prints all the words stored in the Trie.
- It starts from the root and follows each character’s path to print the complete words.
Example:
- If the Trie contains the words "cat", "car", "bat", and "ball", it will print them all.

Sample Output:

Search Results:
Is 'cat' in the Trie? Yes
Is 'car' in the Trie? Yes
Is 'bat' in the Trie? Yes
Is 'ball' in the Trie? Yes
Is 'cow' in the Trie? No

Words in Trie:
ball
bat
car
cat

After deleting 'car':
ball
bat
cat

After deleting 'bat':
ball
cat

Explanation of Output:

Search Results:
- The search operation confirms that "cat", "car", "bat", and "ball" exist in the Trie, while "cow" does not.
Words in Trie:
- Initially, the Trie contains the words "cat", "car", "bat", and "ball".
After Deleting ‘car’:
- The word "car" is deleted, but "cat" remains because the prefix 'c' -> 'a' is shared by both words.
After Deleting ‘bat’:
- The word "bat" is deleted, leaving only "cat" and "ball" in the Trie.

Conclusion

Trie data structures are incredibly powerful when it comes to handling large sets of strings efficiently. Their ability to quickly search for words, suggest prefixes, and handle massive amounts of data makes them ideal for applications like spell-checking, auto-completion, and search engines. However, the trade-off is that they require more memory and may not always be faster than other data structures for exact string matching. Understanding the intricacies of Trie allows you to harness its potential in various real-world scenarios.

Frequently Asked Questions (FAQs) About Trie Data Structure

What is a Trie, and how is it different from other data structures like Hash Tables?

A Trie is a tree-based data structure that is used to store a dynamic set of strings, where the structure is determined by the prefixes of the strings. Unlike Hash Tables, where data is stored in an unordered way using keys and a hashing function, a Trie organizes strings in a hierarchy where nodes represent individual characters.

The major difference between Trie and Hash Tables is in the way they handle prefix-based searches. Trie is extremely efficient when searching for a prefix, because each level of the Trie represents the next character in the string, so you can traverse the tree character by character. In contrast, Hash Tables do not inherently support prefix searches, as they store the data based on the entire key and require additional modifications to perform such operations.

Additionally, Hash Tables offer constant time complexity, O(1), for searching for exact strings, while Trie offers efficient prefix matching with a time complexity of O(k), where k is the length of the string. However, Tries tend to use more memory due to the large number of pointers needed to represent all possible characters at each node.

What are the primary applications of a Trie?

Tries are particularly useful in applications where prefix searches or quick lookup operations are critical. Some common use cases include:

Auto-complete functionality: When a user types a few letters into a search engine or text editor, a Trie can be used to quickly suggest words that begin with that prefix. For example, if the user types “be”, the Trie can return words like “bear”, “bell”, and “bat”.
Spell checkers: Tries are used to store dictionaries in spell-checking programs. When a word is typed, the Trie can quickly determine if the word exists in the dictionary. If not, it can suggest alternatives by analyzing nearby nodes.
Longest Prefix Matching: In networking, Tries are used to match the longest prefix in IP routing. When routing an IP packet, the router looks for the longest matching prefix in its routing table, and a Trie structure efficiently supports this operation.
T9 Texting Systems: Tries were used in early mobile phones for T9 predictive texting, where users pressed keys representing multiple letters, and the Trie helped predict the possible word based on the sequence of key presses.
Data Compression: Tries can be used in algorithms that compress data by recognizing common prefixes among strings, allowing more efficient encoding.

What are the time and space complexities associated with Tries?

The time complexity for common operations in a Trie is as follows:

Insertion: O(k), where k is the length of the word being inserted. Each character is processed in sequence from the root to the leaf.
Search: O(k), where k is the length of the word being searched. The search proceeds character by character down the tree.
Deletion: O(k), where k is the length of the word being deleted. Similar to searching, the word is traversed character by character.

While these time complexities are efficient, Tries tend to have a higher space complexity because each node must store references to all possible child nodes (which could be 26 in the case of the English alphabet, or more in multi-lingual settings).

For a Trie storing n strings, each with an average length of k, the space complexity is O(n * k), where each node potentially has multiple pointers (for each character in the alphabet). Optimizations like compressed tries and ternary search tries are sometimes used to reduce the memory overhead.

How does a Trie perform the insertion of a word?

The insertion operation in a Trie is straightforward and works character by character. Here’s how it works step-by-step:

Start at the root of the Trie.
For each character in the input word:
- Check if there is a node representing that character at the current level of the Trie.
- If such a node exists, move to that node.
- If it doesn’t exist, create a new node for that character and link it to the current node.
Continue this process until you reach the end of the word.
Once the last character is inserted, mark the current node as the end of the word by setting a special flag or marker.

For example, if you’re inserting the word “cat” into an empty Trie, the structure would look like this after insertion:

(root) -- 'c' -- 'a' -- 't' (end of word)

If the word “car” is then inserted, the Trie would share the common “ca” prefix, reducing the need for redundant storage:

(root) -- 'c' -- 'a' -- 't' (end)
                   \
                    'r' (end)

How does searching for a word work in a Trie?

The search operation in a Trie follows the same logic as insertion, but instead of creating new nodes, it simply traverses the existing nodes. The search works as follows:

Start at the root of the Trie.
For each character in the search word:
- Check if there is a node representing that character at the current level.
- If the node exists, move to that node.
- If the node doesn’t exist, the word is not present in the Trie, and the search terminates early.
Continue this process for all characters.
After reaching the last character, check if the node is marked as the end of the word. If it is, the word exists in the Trie.

For example, to search for the word “bat” in a Trie containing “bat”, “ball”, and “bore”, the search would traverse from the root node through the nodes for ‘b’, ‘a’, and ‘t’, confirming that “bat” exists as a complete word.

How does deletion work in a Trie?

The deletion operation in a Trie is more complex than insertion or search because it requires careful handling to ensure that shared prefixes among multiple words aren’t deleted accidentally. The process is as follows:

Search for the word: First, search for the word you want to delete. If the word doesn’t exist in the Trie, exit the operation.
Backtrack: Once the word is found, backtrack from the last character to the root, deleting nodes along the way. However, a node should only be deleted if:
- It is not part of another word (i.e., it has no other children).
- It is not marked as the end of another word.
Mark nodes appropriately: If a node is shared by other words, simply unmark it as the end of the word, but do not delete it.

For example, deleting “bat” from the Trie containing “bat”, “ball”, and “bore” would leave the nodes for ‘b’, ‘a’, and ‘t’ intact, as they are still needed for the words “ball” and “bore”. Only the end-of-word marker for “bat” would be removed.

What are the common types of Trie optimizations?

There are several optimizations to reduce the memory usage and improve the efficiency of Trie:

Compressed Trie (Radix Trie): A compressed Trie reduces memory usage by merging non-branching paths into single nodes. Instead of having one node for each character, a single node can represent multiple characters in a straight path. This is useful when many strings share long prefixes.
Ternary Search Trie: A ternary search Trie is a hybrid between a Trie and a binary search tree. Instead of storing pointers to all possible children (like in a traditional Trie), each node only has three pointers: one to characters less than the current character, one to characters equal to the current character, and one to characters greater than the current character. This structure is more space-efficient for larger alphabets.
Patricia Trie: Also known as a Practical Algorithm to Retrieve Information Coded in Alphanumeric form, this is a type of compressed Trie where nodes with only one child are merged, and each edge is labeled with a string instead of a single character. This further reduces memory usage for long strings.

What are the limitations of a Trie?

While Trie is a powerful and flexible data structure, it has some limitations:

High memory consumption: A traditional Trie can consume a large amount of memory, especially when dealing with large alphabets (e.g., Unicode characters or multi-lingual datasets). Each node needs pointers for every possible character, which can lead to high overhead.
Wasted space with sparse data: If there are very few words or if the words don’t share common prefixes, a lot of memory will be wasted on unused pointers.
Complexity in deletion: Deleting words from a Trie is more complex than in other data structures, as it requires careful management of nodes that may be shared by multiple words.

What is a Ternary Search Trie, and how is it different from a standard Trie?

A Ternary Search Trie is a variation of the traditional Trie that reduces memory usage by using a binary search tree structure at each node. Each node in a Ternary Search Trie has three children:

Left child: Represents characters that are lexicographically smaller than the current character.
Middle child: Represents the next character in the word.
Right child: Represents characters that are lexicographically larger than the current character.

This structure is especially useful when dealing with large alphabets, as it reduces the number of pointers stored at each node. In a traditional Trie, each node could have up to 26 children (for lowercase English letters), but in a Ternary Search Trie, only three-pointers are stored at each node, making it more memory-efficient.

How can Trie be used in network routing for IP address lookup?

In network routing, Trie data structures are used to implement Longest Prefix Matching (LPM), which is a technique used to route packets efficiently. In IP routing, the router needs to find the longest matching prefix for an IP address in its routing table.

Here’s how a Trie helps with this:

The router stores each prefix in a Trie, where each node corresponds to a bit (0 or 1) in the IP address.
To route a packet, the router traverses the Trie bit by bit, following the path that matches the prefix of the IP address.
Once the longest matching prefix is found, the router forwards the packet to the corresponding route.

Tries are particularly efficient for this purpose because they allow the router to quickly find the longest matching prefix, which is crucial for routing high volumes of traffic in real time.

Understanding Trie Data Structure in Depth: A Comprehensive Guide

Table of Contents

What is a Trie Data Structure?

Key Properties of a Trie

Why Use a Trie?

Basic Operations of a Trie

1. Insertion of a Node in a Trie

Explanation of Code:

2. Searching for a Node in a Trie

Explanation of Code:

3. Deletion of a Node in a Trie

Explanation of Code:

Real-World Applications of Trie

Advantages of Trie

Disadvantages of Trie

Implementation of Trie Data Structure In Java Programming Language

Code:

Explanation of Key Steps:

Sample Output:

Explanation of Output:

Implementation of Trie Data Structure In C++ Programming Language

C++ Code Implementation:

Explanation of Key Steps:

1. Node_Trie Class:

2. Trie Class:

Sample Output:

Explanation of Output:

Implementation of Trie Data Structure In Python Programming Language

Python Code Implementation:

Explanation of Key Steps:

1. TrieNode Class:

2. Trie Class:

3. Insert Method:

4. Search Method:

5. Delete Method:

6. print_trie Method:

Sample Output:

Explanation of Output:

Conclusion

Related Articles

Read More Articles

Frequently Asked Questions (FAQs) About Trie Data Structure

What is a Trie, and how is it different from other data structures like Hash Tables?

What are the primary applications of a Trie?

What are the time and space complexities associated with Tries?

How does a Trie perform the insertion of a word?

How does searching for a word work in a Trie?

How does deletion work in a Trie?

What are the common types of Trie optimizations?

What are the limitations of a Trie?

What is a Ternary Search Trie, and how is it different from a standard Trie?

How can Trie be used in network routing for IP address lookup?