Matrix Data Structure: A Comprehensive Guide To The Two-Dimensional Array

Matrix data structures are a fundamental concept in computer science, mathematics, and a wide range of fields like computer graphics, data processing, and linear algebra. They provide an efficient way to store and manipulate data in a structured and organized format. But what exactly is a matrix data structure, how is it used, and why is it so important? This article will cover the various aspects of matrix data structures, including their components, operations, and real-world applications, with detailed examples to provide a deeper understanding of this essential concept.

What is a Matrix Data Structure?

At its core, a matrix is a two-dimensional array or table consisting of rows and columns. Each element in the matrix is located at the intersection of a specific row and column, and this location is referred to as a cell. The data stored in the matrix is distributed across these cells. Matrices are used to store and organize data that can be represented in a grid-like structure. Matrix data structures are especially useful when dealing with tables, grids, or any other structured form of data.

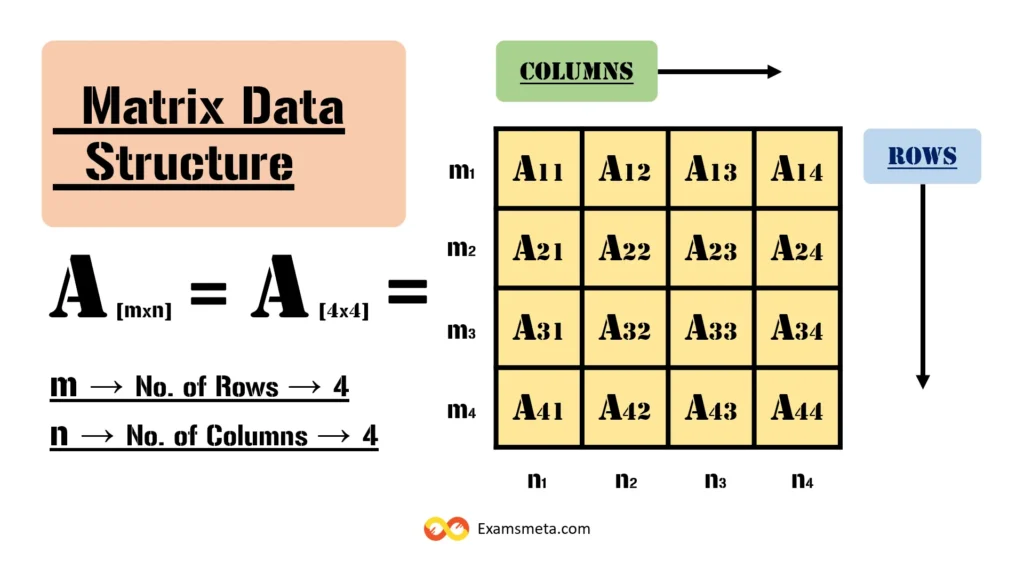
Each element within a matrix is uniquely identified by its row and column indices. For example, in a matrix “A” where the entry at row 1, column 2 is denoted as A[1][2], this helps us easily access, modify, and analyze individual data points.

Components of Matrix Data Structure

Matrices come with various components that define their structure and functionality. Let’s explore each of these components in detail:

Size

The size of a matrix is defined by the number of rows (m) and columns (n) it contains, and is often expressed as an m x n matrix. For example, a 3×4 matrix has 3 rows and 4 columns. The size is an essential factor because it helps determine the type of operations that can be performed on the matrix.

For instance, consider the following matrix:

$$
A = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{bmatrix}
$$

Matrix A has 3 rows and 4 columns, so it is a 3×4 matrix.

Elements

Each individual entry in a matrix is called an element. The elements are identified by their position in the matrix, using the row and column indices. For example, in matrix A:

$$
A[2][3] = 7
$$

This notation means that the element at row 2, column 3 is the number 7.

Scalar Multiplication and Basic Operations

Several basic mathematical operations can be performed on matrices, the most common of which are:

Scalar multiplication: In this operation, each element of the matrix is multiplied by a scalar (a constant value). For example, if we multiply matrix A by 2, the resulting matrix would be:

$$
2 \times A = \begin{bmatrix} 2 & 4 & 6 & 8 \\ 10 & 12 & 14 & 16 \\ 18 & 20 & 22 & 24 \end{bmatrix}
$$

Matrix addition: Two matrices of the same size can be added element-wise. For example, if we have two 2×2 matrices:

$$
B = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, C = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}
$$

The sum would be:

$$
B + C = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix}
$$

Matrix subtraction: Matrix subtraction works similarly to addition, where corresponding elements from two matrices of the same size are subtracted.
Matrix multiplication: Multiplying matrices is more complex than scalar multiplication. In this operation, the number of columns in the first matrix must equal the number of rows in the second matrix. For example, if matrix B is a 2×3 matrix and matrix C is a 3×2 matrix, then their product BC is a 2×2 matrix.

Determinant

The determinant is a scalar value calculated from a square matrix (a matrix with the same number of rows and columns). It is a crucial component in linear algebra because it is used in solving systems of linear equations, determining matrix invertibility, and various other linear transformations.

For example, for a 2×2 matrix B:

$$
B = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
$$

The determinant is calculated as:

$$
det(B) = ad – bc
$$

Inverse

The inverse of a square matrix is another matrix such that when it is multiplied by the original matrix, the result is the identity matrix. Not every matrix has an inverse, but for those that do, the inverse can be used to solve linear equation systems and perform various linear transformations.

For a 2×2 matrix B, the inverse is given by:

$$
B^{-1} = \frac{1}{det(B)} \times \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
$$

This formula applies if det(B) ≠ 0.

Transpose

The transpose of a matrix is obtained by flipping it along its main diagonal, effectively swapping rows with columns. For example, the transpose of matrix A:

$$
A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}
$$

Would be:

$$
A^T = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}
$$

Rank

The rank of a matrix is the number of linearly independent rows or columns. This is a critical concept in solving systems of linear equations and in applications like linear regression analysis.

Common Types of Matrices

There are various specialized types of matrices, each with its unique properties and applications. Some common types include:

Square Matrix: A matrix with an equal number of rows and columns (e.g., 3×3, 4×4).
Diagonal Matrix: A square matrix where all elements except those on the diagonal are zero.
Identity Matrix: A diagonal matrix where all diagonal elements are 1. The identity matrix acts as the multiplicative identity in matrix multiplication.
Zero Matrix: A matrix where all elements are zero.

These matrices simplify many mathematical operations and serve specific purposes in linear algebra, graph theory, and other fields.

Applications of Matrix Data Structure

Linear Algebra

In linear algebra, matrices are widely used to represent linear equations and to solve systems of linear equations. Matrix multiplication, matrix inversion, and determinants play a significant role in various linear transformations.

Optimization

Matrices are crucial in optimization problems like linear programming, where they represent the constraints and objective functions of the system. For example, matrices can be used to express feasible regions and optimize cost or profit in business models.

Statistics

In statistics, matrices are used to organize and manipulate data, particularly in multivariate analysis and regression analysis. For instance, the covariance matrix represents the relationship between multiple variables.

Signal Processing

Matrices are extensively used in signal processing to represent signals and perform operations such as Fourier transforms or filtering. Matrix multiplication is vital in transforming signals from one domain to another.

Network Analysis

In network analysis, matrices are used to represent graphs, where nodes are represented as rows and columns, and the connections (edges) between nodes are represented by matrix elements. This is useful in algorithms for finding the shortest path, maximum flow, and more.

Quantum Mechanics

In quantum mechanics, matrices represent the states and operations in quantum systems. For instance, the Pauli matrices are used to describe the spin of a particle, and the Hamiltonian matrix describes the total energy of a quantum system.

Matrix Data Structure Examples

Below are examples of the Matrix Data Structure implemented as a two-dimensional array in various programming languages, including C++, C, C#, Python, Java, and PHP. Each code will demonstrate the creation of a matrix, basic operations like addition, and the output.

C++ Example: Matrix Addition

#include <iostream>
using namespace std;

int main() {
    // Initialize two 2x2 matrices
    int matrixA[2][2] = {{1, 2}, {3, 4}};
    int matrixB[2][2] = {{5, 6}, {7, 8}};
    int matrixSum[2][2];

    // Adding two matrices
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            matrixSum[i][j] = matrixA[i][j] + matrixB[i][j];
        }
    }

    // Output the result
    cout << "Sum of matrixA and matrixB: " << endl;
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            cout << matrixSum[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

Output:

Sum of matrixA and matrixB:
6 8 
10 12

C Example: Matrix Transpose

#include <stdio.h>

int main() {
    // Initialize a 2x2 matrix
    int matrix[2][2] = {{1, 2}, {3, 4}};
    int transpose[2][2];

    // Transpose the matrix
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            transpose[j][i] = matrix[i][j];
        }
    }

    // Output the transpose
    printf("Transpose of the matrix:\n");
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            printf("%d ", transpose[i][j]);
        }
        printf("\n");
    }

    return 0;
}

Output:

Transpose of the matrix:
1 3 
2 4

C# Example: Matrix Multiplication

using System;

class Program {
    static void Main() {
        int[,] matrixA = { {1, 2}, {3, 4} };
        int[,] matrixB = { {5, 6}, {7, 8} };
        int[,] result = new int[2, 2];

        // Matrix multiplication
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                result[i, j] = 0;
                for (int k = 0; k < 2; k++) {
                    result[i, j] += matrixA[i, k] * matrixB[k, j];
                }
            }
        }

        // Output result
        Console.WriteLine("Product of matrixA and matrixB:");
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                Console.Write(result[i, j] + " ");
            }
            Console.WriteLine();
        }
    }
}

Output:

Product of matrixA and matrixB:
19 22 
43 50

Python Example: Matrix Addition

# Initialize two 2x2 matrices
matrixA = [[1, 2], [3, 4]]
matrixB = [[5, 6], [7, 8]]

# Resultant matrix to store the sum
matrixSum = [[0, 0], [0, 0]]

# Adding two matrices
for i in range(2):
    for j in range(2):
        matrixSum[i][j] = matrixA[i][j] + matrixB[i][j]

# Output the result
print("Sum of matrixA and matrixB:")
for row in matrixSum:
    print(row)

Output:

Sum of matrixA and matrixB:
[6, 8]
[10, 12]

Java Example: Matrix Transpose

public class MatrixTranspose {
    public static void main(String[] args) {
        // Initialize a 2x2 matrix
        int matrix[][] = {{1, 2}, {3, 4}};
        int transpose[][] = new int[2][2];

        // Transpose the matrix
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                transpose[j][i] = matrix[i][j];
            }
        }

        // Output the transpose
        System.out.println("Transpose of the matrix:");
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                System.out.print(transpose[i][j] + " ");
            }
            System.out.println();
        }
    }
}

Output:

Transpose of the matrix:
1 3 
2 4

PHP Example: Matrix Multiplication

<?php
// Initialize two 2x2 matrices
$matrixA = array(
    array(1, 2),
    array(3, 4)
);

$matrixB = array(
    array(5, 6),
    array(7, 8)
);

$matrixProduct = array(
    array(0, 0),
    array(0, 0)
);

// Matrix multiplication
for ($i = 0; $i < 2; $i++) {
    for ($j = 0; $j < 2; $j++) {
        for ($k = 0; $k < 2; $k++) {
            $matrixProduct[$i][$j] += $matrixA[$i][$k] * $matrixB[$k][$j];
        }
    }
}

// Output the result
echo "Product of matrixA and matrixB:\n";
for ($i = 0; $i < 2; $i++) {
    for ($j = 0; $j < 2; $j++) {
        echo $matrixProduct[$i][$j] . " ";
    }
    echo "\n";
}
?>

Output:

Product of matrixA and matrixB:
19 22 
43 50

Conclusion

The matrix data structure is a powerful and versatile tool that underpins many areas of computer science, mathematics, and engineering. From its basic components like size, elements, and operations, to its advanced applications in fields such as linear algebra, statistics, signal processing, and quantum mechanics, matrices play a pivotal role in organizing and manipulating data efficiently.

Understanding matrices allows us to tackle complex problems in data analysis, optimization, and more. Whether you’re working with simple 2×2 matrices or handling massive multi-dimensional arrays in scientific computing, mastering the matrix data structure is an essential step in both academic and professional fields.

Frequently Asked Questions (FAQs) about Matrix Data Structures

What is a Matrix Data Structure?

A Matrix Data Structure is a two-dimensional array organized in rows and columns. Each element in the matrix is identified by its row and column indices. The primary purpose of a matrix is to store data in a structured format, often used for representing mathematical matrices in linear algebra, but it also has significant applications in fields like computer graphics, data processing, and machine learning. Matrices are widely used because they allow efficient manipulation of data for operations such as addition, subtraction, multiplication, and transformations.

For example, a 3×3 matrix with 3 rows and 3 columns can be used to represent geometric transformations in computer graphics, making matrices essential in 3D rendering engines and image processing algorithms.

How do you define the size of a matrix?

The size of a matrix is defined by the number of rows (denoted as “m”) and the number of columns (denoted as “n”). A matrix with m rows and n columns is called an m x n matrix. The size is significant because it determines which mathematical operations can be performed on the matrix.

For instance, a matrix with 2 rows and 3 columns is written as a 2×3 matrix, and its structure would look like this:

$$
\text{Matrix A} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix}
$$

This 2×3 matrix has two rows (with subscripts 1 and 2) and three columns (with subscripts 1, 2, and 3).

What are the most common operations on matrices?

Several important mathematical operations are performed on matrices. The most common are:

Matrix Addition: You can add two matrices if they have the same size. Each element in the resulting matrix is the sum of the corresponding elements from the original matrices. For example: $$
\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix}
$$
Matrix Subtraction: Similar to addition, matrices must be the same size to subtract corresponding elements.
Matrix Multiplication: In this operation, the number of columns in the first matrix must equal the number of rows in the second matrix. This is more complex and involves computing the dot product of rows from the first matrix with columns from the second.
Scalar Multiplication: Each element of the matrix is multiplied by a scalar (a constant value).
Transpose: The transpose of a matrix is obtained by swapping its rows and columns, i.e., flipping it over its diagonal. If A is the matrix, its transpose is denoted A^T.

What is the importance of the Determinant in a Matrix?

The determinant is a scalar value associated with square matrices (matrices that have the same number of rows and columns). The determinant provides essential information about the matrix, such as whether it is invertible or not. A matrix is invertible (i.e., it has an inverse) if and only if its determinant is non-zero.

The determinant also has applications in solving systems of linear equations, calculating the area or volume in geometry, and transforming vectors in linear algebra. For example, if a matrix represents a transformation, the absolute value of its determinant tells us whether the transformation preserves or changes the orientation of the geometric object.

For a 2×2 matrix:

$$
\text{Matrix B} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
$$

The determinant is calculated as:

det(B) = ad – bc

How is the inverse of a matrix calculated?

The inverse of a matrix is another matrix that, when multiplied by the original matrix, results in the identity matrix. Not all matrices have an inverse; a matrix has an inverse only if its determinant is non-zero.

For a 2×2 matrix:

$$
\text{Matrix B} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
$$

The inverse of B, denoted as B^{-1}, is given by:

$$
B^{-1} = \frac{1}{ad – bc} \times \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
$$

This formula only works if the determinant (ad – bc) is non-zero.

For larger matrices, finding the inverse involves more complex methods such as Gaussian elimination or the adjoint method.

What is the Rank of a matrix?

The rank of a matrix is the maximum number of linearly independent rows or columns within the matrix. Rank helps determine whether a system of linear equations has a unique solution, no solution, or infinitely many solutions.

For example, a matrix with full rank means all of its rows (or columns) are linearly independent, implying that the matrix spans the full vector space. Rank plays a crucial role in fields such as linear regression, machine learning, and signal processing.

How is the transpose of a matrix useful?

The transpose of a matrix is created by flipping the matrix along its main diagonal, essentially switching rows and columns. It is useful in many applications such as solving systems of equations, in graph theory, and in machine learning for performing matrix factorizations.

For example, in linear algebra, the transpose of a matrix can be used to change the dimensions of a vector or matrix, making it easier to perform dot products and other matrix operations.

Given a matrix:

$$
A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}
$$

Its transpose would be:

$$
A^T = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}
$$

What are some special types of matrices?

Matrices come in different types, each with unique properties:

Square Matrix: A matrix with an equal number of rows and columns (e.g., a 3×3 matrix).
Diagonal Matrix: A square matrix where all off-diagonal elements are zero (i.e., only the elements on the main diagonal are non-zero).
Identity Matrix: A square matrix in which all diagonal elements are 1, and all other elements are 0. The identity matrix is the multiplicative identity in matrix multiplication.
Zero Matrix: A matrix in which all elements are zero.
Symmetric Matrix: A matrix that is equal to its transpose, i.e., A = A^T.

Each of these matrices has specific applications in linear algebra, machine learning, and graph theory.

How are matrices used in computer graphics?

Matrices are fundamental in computer graphics for transforming and manipulating 2D and 3D objects. They are used to perform operations such as rotation, scaling, translation, and perspective projection.

For example, a transformation matrix can be applied to a set of coordinates to rotate an object in 3D space. Similarly, scaling matrices can resize objects, while translation matrices shift them from one location to another. These matrices are essential in 3D rendering engines and graphics software like OpenGL and DirectX.

What is the role of matrices in linear algebra?

In linear algebra, matrices are used to represent systems of linear equations, perform linear transformations, and describe geometric properties like rotation and scaling. Matrices allow us to easily manipulate multiple equations and variables at once, making them a powerful tool in solving real-world problems like economic modeling, engineering, and physics.

Matrices are also crucial for representing transformations between different coordinate systems in vector spaces.

What is the application of matrices in machine learning?

In machine learning, matrices are used to represent data sets and perform mathematical operations essential for training models. For example:

Data Representation: Rows in a matrix can represent different data samples, while columns represent features of the samples. A training data set is typically organized in matrix form.
Linear Regression: Matrices are used to solve linear regression problems where the aim is to find the best fit line through data points by minimizing the error between predicted and actual outcomes.
Neural Networks: In deep learning, matrices represent the weights of connections between neurons in different layers of a neural network. Matrix operations such as multiplication are crucial in propagating information through the network.

How are matrices used in signal processing?

In signal processing, matrices represent signals as discrete samples and matrix operations such as Fourier transforms are used to analyze and process signals. Matrix decompositions such as the Singular Value Decomposition (SVD) help in filtering noise from signals and compressing data.

For instance, the discrete Fourier transform (DFT) can be expressed in matrix form, allowing efficient manipulation of signals for audio and image processing.

How are matrices applied in statistics?

In statistics, matrices are used to organize data and perform operations like regression analysis, correlation, and covariance calculations. For instance, in multivariate analysis, a covariance matrix describes how variables in a data set relate to each other.

For example, a correlation matrix helps in understanding the relationships between multiple variables, indicating whether variables move together (positive correlation) or in opposite directions (negative correlation).

What role do matrices play in network analysis?

In network analysis, matrices are used to represent the structure of graphs and networks. The most common type is the adjacency matrix, which represents whether pairs of nodes in a graph are connected. If there is an edge between two nodes, the corresponding cell in the adjacency matrix contains a 1; otherwise, it contains a 0.

This matrix is essential in solving problems like finding the shortest path between nodes or determining the degree of nodes in the network.

How are matrices used in quantum mechanics?

In quantum mechanics, matrices, specifically Hermitian matrices, represent observables (measurable quantities like position, momentum, and energy). The state of a quantum system is often represented as a vector, and matrix operations are used to describe the evolution of the system over time.

For instance, the Hamiltonian matrix represents the total energy of a system, and applying it to a state vector gives information about the system’s dynamics. Matrices are essential in quantum computing as well, where they represent the transformation of quantum states.

Matrix Data Structure: A Comprehensive Guide to the Two-Dimensional Array

Table of Contents

What is a Matrix Data Structure?

Components of Matrix Data Structure

Size

Elements

Scalar Multiplication and Basic Operations

Determinant

Inverse

Transpose

Rank

Common Types of Matrices

Applications of Matrix Data Structure

Linear Algebra

Optimization

Statistics

Signal Processing

Network Analysis

Quantum Mechanics

Matrix Data Structure Examples

C++ Example: Matrix Addition

C Example: Matrix Transpose

C# Example: Matrix Multiplication

Python Example: Matrix Addition

Java Example: Matrix Transpose

PHP Example: Matrix Multiplication

Conclusion

Related Articles

Read More Articles

Frequently Asked Questions (FAQs) about Matrix Data Structures

What is a Matrix Data Structure?

How do you define the size of a matrix?

What are the most common operations on matrices?

What is the importance of the Determinant in a Matrix?

How is the inverse of a matrix calculated?

What is the Rank of a matrix?

How is the transpose of a matrix useful?

What are some special types of matrices?

How are matrices used in computer graphics?

What is the role of matrices in linear algebra?

What is the application of matrices in machine learning?

How are matrices used in signal processing?

How are matrices applied in statistics?

What role do matrices play in network analysis?

How are matrices used in quantum mechanics?