Understanding Linear Data Structures: A Comprehensive Exploration

In the realm of Computer Science, data structures serve as the backbone of efficient data management and organization. These structures are the building blocks that allow us to store, access, and modify data with ease. Among these, linear data structures hold a special place, as they offer simplicity in their design and ease of implementation. Linear data structures are characterized by their sequential organization, where each element is connected to its preceding and succeeding elements, forming a straight line. In this post, we will explore some of the most widely used linear data structures: Arrays, Stacks, Queues, Linked Lists, and Hash Tables.

What Are Linear Data Structures?

A linear data structure is a type of data organization in which elements are arranged in a sequential manner, meaning one after the other. In these structures, there is a clear beginning and end, and each element is connected to its neighboring elements. What makes linear data structures simple and easy to work with is that you can traverse the entire data set in a single run. The sequential nature of these structures allows for predictable memory usage and access patterns, which is why they are favored in various programming applications.

Linear Data Structures One Dimensional Array — Linear Data Structures, One Dimensional Array

The key characteristic of linear structures is that there is only one path to access any element, unlike non-linear data structures like trees or graphs, which can have multiple paths. This unique attribute makes linear data structures straightforward to implement and manage, especially for tasks where a sequence of operations needs to be performed.

Now, let’s delve deeper into some of the most prominent types of linear data structures and explore their functionalities in greater detail.

1. Arrays: The Building Blocks of Data Storage

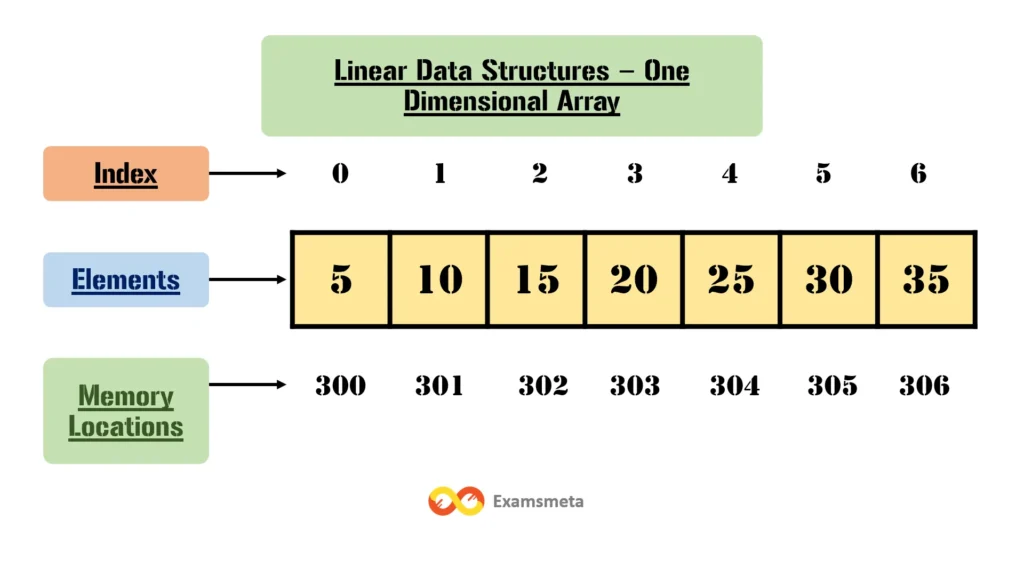
An array is the most fundamental type of data structure and is used extensively in Computer Science. It stores elements of the same data type in contiguous memory locations, meaning all elements are stored one after the other in a block of memory. Arrays allow random access to data, meaning you can directly access any element in the array using its index, which acts as a pointer to a specific memory location.

Example:

Consider a scenario where we need to store the prices of ten different cars. Instead of creating ten separate variables, we can create an array to hold all the prices together in a structured format. Each element in the array is accessible by its index, starting from index 0 for the first element.

car_prices = [20000, 25000, 18000, 30000, 27000, 32000, 15000, 29000, 24000, 31000]

# Access the price of the fifth car
print(car_prices[4])  # Output: 27000

This is far more efficient than creating ten separate variables, as it saves both time and memory. Arrays are particularly useful in situations where we need random access to data, as any element can be accessed directly using its index.

However, arrays come with certain limitations:

Limitations of Arrays:

Fixed Size: Once declared, the size of an array cannot be changed. This means that arrays have a static size, making it difficult to accommodate varying amounts of data. For instance, if we declare an array of size 10, we cannot store 11 elements in it without recreating the entire array.
Homogeneous Elements: All elements in an array must be of the same data type. For example, if we declare an array to store integers, we cannot store floats or strings in it. This limitation can be restrictive in certain applications where a mix of data types is required.

Applications of Arrays:

Arrays are widely used in situations where data is relatively static and requires random access. Some common applications include:

Storing records in databases where each record has the same data type.
Implementing lookup tables where the index corresponds to specific values.
Multidimensional arrays in scientific computations, such as matrices.

2. Stacks: Last In, First Out (LIFO) Structure

A stack is another linear data structure that operates on the principle of Last In, First Out (LIFO). This means that the last element added to the stack is the first one to be removed. A stack can be visualized like a stack of books, where you can only add or remove the topmost book. You cannot access any element that is not on the top without first removing the elements above it.

Main Operations in a Stack:

Push: Adds an element to the top of the stack.
Pop: Removes the element from the top of the stack.

Example of Stack Operations:

Consider a stack representing a set of web pages visited during a browsing session. Each time you visit a new page, it is “pushed” onto the stack. When you click the “back” button, the most recent page is “popped” from the stack.

stack = []

# Push elements onto the stack
stack.append("Page 1")
stack.append("Page 2")
stack.append("Page 3")

# Pop the last element
last_page = stack.pop()
print(last_page)  # Output: Page 3

Applications of Stacks:

Undo operations in text editors: Each action you perform is pushed onto the stack, and when you press “undo,” the last action is popped from the stack.
Recursion: Stacks are used to keep track of function calls in recursive programming.
Expression evaluation: In postfix or prefix notation, stacks are used to evaluate mathematical expressions.
Syntax parsing: Stacks play a crucial role in parsing programming languages, where they manage the opening and closing of parentheses, brackets, and braces.

3. Queues: First In, First Out (FIFO) Structure

A queue is similar to a stack, but it follows the principle of First In, First Out (FIFO). In a queue, the first element added is the first one to be removed. This can be compared to a line of people waiting for their turn—those who arrive first are served first. Unlike stacks, where you can only access the top element, queues allow access to both the front and rear ends.

Main Operations in a Queue:

Enqueue: Adds an element to the rear of the queue.
Dequeue: Removes an element from the front of the queue.

Example of Queue Operations:

Imagine a scenario where customers are waiting in line at a bank. The first customer to arrive is served first, and each subsequent customer is served in the order they arrive.

queue = []

# Enqueue elements
queue.append("Customer 1")
queue.append("Customer 2")
queue.append("Customer 3")

# Dequeue the first customer
first_customer = queue.pop(0)
print(first_customer)  # Output: Customer 1

Types of Queues:

Circular Queue: In a circular queue, the last element is connected back to the first element, forming a circle. This is particularly useful in resource scheduling where processes need to be cycled through continuously.
Priority Queue: In a priority queue, each element has a priority, and elements with higher priority are dequeued before those with lower priority, regardless of their arrival order.
Deque (Double-Ended Queue): A deque allows insertion and deletion from both ends (front and rear).

Applications of Queues:

Scheduling systems: In operating systems, queues are used to manage tasks and allocate CPU time.
Printer queues: Documents are printed in the order they are submitted.
Breadth-first search (BFS): Queues are used in the BFS algorithm to explore nodes level by level in a graph or tree.

4. Linked Lists: Dynamic Memory Allocation

A linked list is a dynamic data structure where each element, called a node, contains two parts: the data and a pointer (or reference) to the next node in the sequence. Unlike arrays, linked lists are not stored in contiguous memory locations. This allows linked lists to grow and shrink in size as needed during the execution of a program, providing flexibility in memory allocation.

Types of Linked Lists:

Singly Linked List: In this type of linked list, each node points to the next node in the sequence. The last node points to None indicate the end of the list.
Doubly Linked List: Each node points to both the next node and the previous node. This allows traversal in both directions.
Circular Linked List: In a circular linked list, the last node points back to the first node, forming a circular structure.

Example of Linked List:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

# Create nodes
node1 = Node(10)
node2 = Node(20)
node3 = Node(30)

# Link nodes
node1.next = node2
node2.next = node3

# Traverse linked list
current_node = node1
while current_node is not None:
    print(current_node.data)
    current_node = current_node.next

Applications of Linked Lists:

Dynamic memory allocation: Linked lists are ideal for situations where the data set may change in size during execution.
Implementation of stacks and queues: Linked lists can be used to implement stacks and queues, providing dynamic memory management.
Graph data structures: In graph algorithms, linked lists are often used to represent adjacency lists.

5. Hash Tables: Fast Lookups with Key-Value Pairs

Although not strictly a linear data structure, hash tables are sometimes classified as such due to their ability to store data in an array-like fashion. A hash table is a data structure that stores data in key-value pairs, where each key is processed through a hash function to compute a unique index (or hash) that determines where the value will be stored in memory.

Example of Hash Table:

hash_table = {}

# Insert key-value pairs
hash_table["apple"] = 50
hash_table["banana"] = 30
hash_table["orange"] = 20

# Access a value by key
print(hash_table["banana"])  # Output: 30

Applications of Hash Tables:

Dictionaries: Hash tables are commonly used to implement dictionaries, where words are mapped to definitions.
Databases: In database management systems, hash tables are used to implement indexes for fast data retrieval.
Caching: Hash tables are used in caching mechanisms to store frequently accessed data.

Examples Based on Linear Data Structures

Here are comprehensive coding examples of Linear Data Structures: Arrays, Stacks, Queues, Linked Lists, and Hash Tables implemented in C++, C, Python, Java, and JavaScript. Each example includes the input, code, and output to give you a clear understanding of how each data structure works in these different languages.

Array Implementation

C++ Example

#include<iostream>
using namespace std;

int main() {
    // Declare and initialize an array
    int arr[5] = {10, 20, 30, 40, 50};

    // Access and display elements using a loop
    for(int i = 0; i < 5; i++) {
        cout << "Element at index " << i << ": " << arr[i] << endl;
    }

    return 0;
}

Output:

Element at index 0: 10
Element at index 1: 20
Element at index 2: 30
Element at index 3: 40
Element at index 4: 50

Python Example

# Declare and initialize an array
arr = [10, 20, 30, 40, 50]

# Access and display elements using a loop
for i in range(len(arr)):
    print(f"Element at index {i}: {arr[i]}")

Output:

Element at index 0: 10
Element at index 1: 20
Element at index 2: 30
Element at index 3: 40
Element at index 4: 50

Java Example

public class ArrayExample {
    public static void main(String[] args) {
        // Declare and initialize an array
        int[] arr = {10, 20, 30, 40, 50};

        // Access and display elements using a loop
        for (int i = 0; i < arr.length; i++) {
            System.out.println("Element at index " + i + ": " + arr[i]);
        }
    }
}

Output:

Element at index 0: 10
Element at index 1: 20
Element at index 2: 30
Element at index 3: 40
Element at index 4: 50

JavaScript Example

// Declare and initialize an array
let arr = [10, 20, 30, 40, 50];

// Access and display elements using a loop
for (let i = 0; i < arr.length; i++) {
    console.log(`Element at index ${i}: ${arr[i]}`);
}

Output:

Element at index 0: 10
Element at index 1: 20
Element at index 2: 30
Element at index 3: 40
Element at index 4: 50

2. Stack Implementation

C++ Example

#include<iostream>
#include<stack>
using namespace std;

int main() {
    stack<int> stk;

    // Push elements onto the stack
    stk.push(10);
    stk.push(20);
    stk.push(30);

    // Pop and display elements
    while(!stk.empty()) {
        cout << "Popped element: " << stk.top() << endl;
        stk.pop();
    }

    return 0;
}

Output:

Popped element: 30
Popped element: 20
Popped element: 10

Python Example

# Initialize stack
stack = []

# Push elements onto the stack
stack.append(10)
stack.append(20)
stack.append(30)

# Pop and display elements
while stack:
    print(f"Popped element: {stack.pop()}")

Output:

Popped element: 30
Popped element: 20
Popped element: 10

Java Example

import java.util.Stack;

public class StackExample {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();

        // Push elements onto the stack
        stack.push(10);
        stack.push(20);
        stack.push(30);

        // Pop and display elements
        while (!stack.isEmpty()) {
            System.out.println("Popped element: " + stack.pop());
        }
    }
}

Output:

Popped element: 30
Popped element: 20
Popped element: 10

JavaScript Example

// Initialize stack
let stack = [];

// Push elements onto the stack
stack.push(10);
stack.push(20);
stack.push(30);

// Pop and display elements
while (stack.length > 0) {
    console.log(`Popped element: ${stack.pop()}`);
}

Output:

Popped element: 30
Popped element: 20
Popped element: 10

3. Queue Implementation

C++ Example

#include<iostream>
#include<queue>
using namespace std;

int main() {
    queue<int> q;

    // Enqueue elements
    q.push(10);
    q.push(20);
    q.push(30);

    // Dequeue and display elements
    while(!q.empty()) {
        cout << "Dequeued element: " << q.front() << endl;
        q.pop();
    }

    return 0;
}

Output:

Dequeued element: 10
Dequeued element: 20
Dequeued element: 30

Python Example

from collections import deque

# Initialize queue
queue = deque()

# Enqueue elements
queue.append(10)
queue.append(20)
queue.append(30)

# Dequeue and display elements
while queue:
    print(f"Dequeued element: {queue.popleft()}")

Output:

Dequeued element: 10
Dequeued element: 20
Dequeued element: 30

Java Example

import java.util.LinkedList;
import java.util.Queue;

public class QueueExample {
    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>();

        // Enqueue elements
        queue.add(10);
        queue.add(20);
        queue.add(30);

        // Dequeue and display elements
        while (!queue.isEmpty()) {
            System.out.println("Dequeued element: " + queue.poll());
        }
    }
}

Output:

Dequeued element: 10
Dequeued element: 20
Dequeued element: 30

JavaScript Example

// Initialize queue
let queue = [];

// Enqueue elements
queue.push(10);
queue.push(20);
queue.push(30);

// Dequeue and display elements
while (queue.length > 0) {
    console.log(`Dequeued element: ${queue.shift()}`);
}

Output:

Dequeued element: 10
Dequeued element: 20
Dequeued element: 30

4. Linked List Implementation

C Example

#include <stdio.h>
#include <stdlib.h>

// Define node structure
struct Node {
    int data;
    struct Node* next;
};

// Function to print linked list
void printList(struct Node* n) {
    while (n != NULL) {
        printf("%d -> ", n->data);
        n = n->next;
    }
    printf("NULL\n");
}

// Main function
int main() {
    struct Node* head = NULL;
    struct Node* second = NULL;
    struct Node* third = NULL;

    // Allocate nodes in the heap
    head = (struct Node*)malloc(sizeof(struct Node));
    second = (struct Node*)malloc(sizeof(struct Node));
    third = (struct Node*)malloc(sizeof(struct Node));

    // Initialize nodes
    head->data = 1;
    head->next = second;

    second->data = 2;
    second->next = third;

    third->data = 3;
    third->next = NULL;

    // Print the linked list
    printList(head);

    return 0;
}

Output:

1 -> 2 -> 3 -> NULL

Python Example

# Define the node structure
class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

# Function to print linked list
def print_list(node):
    while node:
        print(f"{node.data} -> ", end="")
        node = node.next
    print("NULL")

# Initialize linked list nodes
head = Node(1)
second = Node(2)
third = Node(3)

# Link the nodes
head.next = second
second.next = third

# Print the linked list
print_list(head)

Output:

1 -> 2 -> 3 -> NULL

5. Hash Table Implementation

Python Example

# Initialize hash table as a dictionary
hash_table = {}

# Insert key-value pairs
hash_table["apple"] = 50
hash_table["banana"] = 30
hash_table["orange"] = 20

# Access and display key-value pairs
for key, value in hash_table

.items():
    print(f"{key}: {value}")

Output:

apple: 50
banana: 30
orange: 20

Java Example

import java.util.HashMap;

public class HashTableExample {
    public static void main(String[] args) {
        HashMap<String, Integer> hashTable = new HashMap<>();

        // Insert key-value pairs
        hashTable.put("apple", 50);
        hashTable.put("banana", 30);
        hashTable.put("orange", 20);

        // Access and display key-value pairs
        for (String key : hashTable.keySet()) {
            System.out.println(key + ": " + hashTable.get(key));
        }
    }
}

Output:

apple: 50
banana: 30
orange: 20

Conclusion

Linear data structures like arrays, stacks, queues, linked lists, and hash tables are the fundamental building blocks of efficient algorithms and data storage mechanisms in Computer Science. Each data structure has its unique advantages, limitations, and areas of application, making them suitable for different types of tasks. Understanding the behavior, operations, and use cases of these structures is crucial for writing efficient programs and solving complex computational problems.

Frequently Asked Questions (FAQs) on Linear Data Structures

What is a Linear Data Structure?

A linear data structure is a type of data structure where elements are arranged sequentially, one after the other. In other words, there is a clear ordering of elements, and each element is connected to its preceding and succeeding elements. The most crucial characteristic is that there is only a single path to traverse or access any element in the structure.

For example, in an array, each element has a fixed position, and accessing the next element involves moving linearly to the following index. Similarly, in a stack, elements are added and removed in a linear order (LIFO), and in a queue, they are processed in a FIFO order. Linear data structures are simple to implement and ideal for situations where we need to perform sequential operations.

How is an Array different from other Linear Data Structures?

An array is a contiguous block of memory that stores elements of the same data type. The key difference between arrays and other linear data structures like linked lists, stacks, or queues is that arrays allow random access to any element. This means that given an index, you can access any element in constant time (O(1)).

On the other hand, structures like linked lists require traversal to access specific elements, and structures like stacks and queues restrict access to only the top (for stacks) or front/ rear (for queues) elements.

What are the advantages of using Arrays?

Arrays offer several advantages:

Random Access: You can access any element directly using its index in constant time.
Memory Efficiency: Arrays are memory efficient because they use a contiguous block of memory.
Simplicity: Arrays are easy to implement and use, making them the go-to data structure for simple, ordered collections of data.
Cache Optimization: Due to their contiguous memory layout, arrays can be more efficient when accessed sequentially because modern CPU caches can prefetch subsequent elements.

However, arrays have limitations, such as their fixed size and the requirement for homogeneous elements.

What is a Stack, and how does it work?

A stack is a Last In, First Out (LIFO) data structure, meaning that the last element added to the stack is the first one to be removed. Stacks are like a pile of books where you can only add or remove the topmost book. You cannot access elements in the middle without first removing those above it.

There are two main operations in a stack:

Push: Adds an element to the top of the stack.
Pop: Removes the element from the top of the stack.

Stacks are widely used in recursive algorithms, undo operations in text editors, and syntax parsing.

How do Queues differ from Stacks?

While both queues and stacks are linear data structures, their primary difference lies in how they manage elements. A queue follows the First In, First Out (FIFO) principle, meaning the first element added to the queue is the first one to be removed. In contrast, a stack operates on LIFO, where the last element added is the first to be removed.

In a queue, you perform two main operations:

Enqueue: Add an element to the end (rear) of the queue.
Dequeue: Remove an element from the front (front) of the queue.

Queues are commonly used in task scheduling and breadth-first search (BFS) algorithms.

What are some real-world applications of Stacks?

Stacks are used in many real-world applications, especially in scenarios where reversibility or backtracking is required. Some of the most common applications include:

Undo functionality in text editors or applications: Each action is pushed onto the stack, and pressing “undo” pops the most recent action.
Recursion: When a function calls itself, the function calls are stored in a stack, allowing the program to resume after the recursive call finishes.
Browser history: Browsers use stacks to store visited pages. When you click the “back” button, the most recent page pops up from the stack.
Expression evaluation: Stacks are used to evaluate postfix and prefix expressions in mathematical computations.

What are some real-world applications of Queues?

Queues are widely used in applications that require sequential processing of tasks. Some examples include:

Print queues: Documents are printed in the order they are submitted.
Task scheduling: In operating systems, tasks are scheduled in a queue based on their arrival time. This ensures that the first task to arrive is the first one to be executed.
Call centers: Incoming customer calls are queued up and handled in the order they arrive.
Breadth-First Search (BFS): In graph traversal algorithms like BFS, a queue is used to explore nodes level by level.

What is a Linked List?

A linked list is a linear data structure where elements, known as nodes, are linked using pointers. Each node contains two parts: the data and a pointer to the next node in the sequence. Unlike arrays, linked lists are dynamic in size, meaning they can grow and shrink as needed during program execution.

There are several types of linked lists:

Singly Linked List: Each node points to the next node.
Doubly Linked List: Each node points to both the next and previous nodes.
Circular Linked List: The last node points back to the first node, forming a circular chain.

How does a Linked List differ from an Array?

Arrays and linked lists both store elements sequentially, but they differ in several key ways:

Memory Allocation: Arrays use contiguous memory locations, whereas linked lists use non-contiguous memory. Each element in a linked list points to the next, allowing the list to expand dynamically.
Access Time: In an array, you can access any element in constant time (O(1)) by using its index. In contrast, in a linked list, you must traverse the list from the head to access a specific element, resulting in an access time of O(n).
Insertion and Deletion: Linked lists allow for faster insertion and deletion, especially at the beginning or middle of the list, as you don’t need to shift elements like in an array.

What are the benefits of using a Linked List?

Linked Lists offer several advantages:

Dynamic Size: Linked lists can grow and shrink dynamically during program execution, making them ideal for applications where the size of the data set changes frequently.
Efficient Insertions/Deletions: Inserting or deleting elements at the beginning or middle of a linked list is more efficient than in an array because there’s no need to shift elements.
Memory Efficiency: Linked lists use memory only for the nodes currently being stored, unlike arrays which reserve memory for a fixed size.

However, the downside is that linked lists do not offer random access and require more memory per element due to the pointers.

What is a Circular Linked List, and where is it used?

A Circular Linked List is a variation of a linked list where the last node points back to the first node, forming a circular structure. This means that starting from any node, you can traverse the entire list without reaching the end.

Applications of Circular Linked Lists:

Round-robin scheduling: In operating systems, circular linked lists are used in round-robin task scheduling to cycle through processes in a fair manner.
Buffer Management: In networking or multimedia systems, circular buffers (implemented using circular linked lists) manage streaming data that loops continuously.

What is a Doubly Linked List, and how does it differ from a Singly Linked List?

A Doubly Linked List is a type of linked list where each node contains two pointers: one pointing to the next node and the other pointing to the previous node. This allows traversal in both directions (forward and backward).

The primary difference between a Singly Linked List and a Doubly Linked List is that in a singly linked list, you can only traverse in one direction, while in a doubly linked list, you can traverse in both directions. This added flexibility makes doubly linked lists more useful in applications like navigation systems, where forward and backward traversal is required.

What is a Hash Table, and how does it work?

A Hash Table is a data structure that stores elements in key-value pairs. The key is processed through a hash function to compute a unique index, called a hash, where the corresponding value will be stored in memory.

Hash Function:

The efficiency of a hash table depends on the quality of its hash function, which should distribute keys evenly across the available slots to avoid collisions.

Collisions:

When two keys produce the same hash, a collision occurs. Hash tables handle collisions through techniques like chaining (storing collided elements in a linked list) or open addressing (probing for the next available slot).

What are some common applications of Hash Tables?

Hash Tables are used in various applications where fast lookups are required. Some common use cases include:

Dictionaries: In a dictionary, words (keys) are mapped to their definitions (values).
Database Indexing: In databases, hash tables are used for indexing to allow quick access to rows in a table.
Caching: Web browsers and other systems use hash tables to store frequently accessed data for faster retrieval.

What is the time complexity of common operations on Arrays?

The time complexity of various operations on arrays depends on the specific operation:

Access: O(1) (Constant time) – Accessing an element by its index takes constant time.
Search: O(n) (Linear time) – Searching for an element requires scanning the array, which takes linear time in the worst case.
Insertion/Deletion: O(n) – Inserting or deleting elements requires shifting the remaining elements, leading to linear time complexity.

What is the time complexity of common operations on Linked Lists?

In a linked list, the time complexity for different operations varies:

Access/Search: O(n) – To access or search for an element, you need to traverse the list from the head to the desired node.
Insertion/Deletion: O(1) – Inserting or deleting at the beginning of the list is a constant-time operation since no elements need to be shifted.

What are the different types of Queues?

There are several types of queues, each designed for specific use cases:

Simple Queue: Operates on a First In, First Out (FIFO) principle.
Circular Queue: In a circular queue, the last position is connected back to the first, forming a circle. This helps efficiently utilize storage.
Priority Queue: In a priority queue, elements are dequeued based on their priority, rather than the order in which they were enqueued.
Deque (Double-Ended Queue): A deque allows insertion and deletion from both the front and the rear.

How does a Priority Queue differ from a Normal Queue?

In a Priority Queue, each element has a priority level. Elements are dequeued not based on their order of arrival but according to their priority. If two elements have the same priority, they are dequeued based on FIFO.

Priority queues are commonly used in task scheduling (where urgent tasks are executed first) and in graph algorithms like Dijkstra’s shortest path.

What is the difference between a Stack and a Queue?

A Stack is a LIFO data structure where the last element added is the first one removed. A Queue, on the other hand, is a FIFO structure where the first element added is the first one removed.

Stack Operations: Push (add to top) and Pop (remove from top).
Queue Operations: Enqueue (add to rear) and Dequeue (remove from front).

When should I use a Hash Table over an Array?

Use a Hash Table when you need fast lookups, insertions, and deletions in constant time (O(1) on average). Arrays are better suited for situations where you need to access elements by index quickly or when the size of the data set is fixed.

Hash tables are ideal for applications like dictionaries, caches, and indexing in databases, while arrays are preferable for fixed-sized collections or when performing sequential access on data.

Understanding Linear Data Structures: A Comprehensive Exploration

Table of Contents

What Are Linear Data Structures?

1. Arrays: The Building Blocks of Data Storage

Example:

Limitations of Arrays:

Applications of Arrays:

2. Stacks: Last In, First Out (LIFO) Structure

Main Operations in a Stack:

Example of Stack Operations:

Applications of Stacks:

3. Queues: First In, First Out (FIFO) Structure

Main Operations in a Queue:

Example of Queue Operations:

Types of Queues:

Applications of Queues:

4. Linked Lists: Dynamic Memory Allocation

Types of Linked Lists:

Example of Linked List:

Applications of Linked Lists:

5. Hash Tables: Fast Lookups with Key-Value Pairs

Example of Hash Table:

Applications of Hash Tables:

Examples Based on Linear Data Structures

Array Implementation

C++ Example

Python Example

Java Example

JavaScript Example

2. Stack Implementation

C++ Example

Python Example

Java Example

JavaScript Example

3. Queue Implementation

C++ Example

Python Example

Java Example

JavaScript Example

4. Linked List Implementation

C Example

Python Example

5. Hash Table Implementation

Python Example

Java Example

Conclusion

Related Articles

Read More Articles

Frequently Asked Questions (FAQs) on Linear Data Structures

What is a Linear Data Structure?

How is an Array different from other Linear Data Structures?

What are the advantages of using Arrays?

What is a Stack, and how does it work?

How do Queues differ from Stacks?

What are some real-world applications of Stacks?

What are some real-world applications of Queues?

What is a Linked List?

How does a Linked List differ from an Array?

What are the benefits of using a Linked List?

What is a Circular Linked List, and where is it used?

Applications of Circular Linked Lists:

What is a Doubly Linked List, and how does it differ from a Singly Linked List?

What is a Hash Table, and how does it work?

Hash Function:

Collisions:

What are some common applications of Hash Tables?

What is the time complexity of common operations on Arrays?

What is the time complexity of common operations on Linked Lists?

What are the different types of Queues?

How does a Priority Queue differ from a Normal Queue?

What is the difference between a Stack and a Queue?

When should I use a Hash Table over an Array?